ABCDEF is a regular hexagon with point O as centre. The value of −−→AB+−−→AC+−−→AD+−−→AE+−−→AF is
−−→AO
2−−→AO
4−−→AO
6−−→AO
The correct Answer is:D
−−→AB+−−→AC+−−→AD+−−→AE+−−→AF=−−→OA+−−→OA+2−−→OA+−−→OA+−−→OA=6(−−→OA)=6(−−→AO)
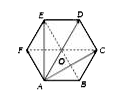
−−→AC=−−→AO
[angle between −−→ABand−−→BC is 120∘]

Similar Questions
ABCDEF is a regular hexagon with point O as centre. Find the value of −−→AB+−−→AC+−−→AD+−−→AE+−−→AF
 06:21View Solution
06:21View SolutionABCDEF is a regular hexagon with point O as centre. Find the value of −−→AB+−−→AC+−−→AD+−−→AE+−−→AF
 06:21View Solution
06:21View SolutionABCDEF is a regular hexagon. Find the vector →AB+→AC+→AD+→AE+→AF in terms of the vector →AD
06:13View SolutionABCDEF is a regular hexagon with point O as centre. Find the value of −−→AB+−−→AC+−−→AD+−−→AE+−−→AF
 06:21View Solution
06:21View SolutionABCDEF is a regular hexagon, Fig. 2 (c ) .65. What is the value of (vec (AB) + vec (AC) + vec (AD) + vec (AE) + vec (AF) ? .
05:00View SolutionABCDEF is a regular hexagon with point O as centre. Find the value of vec(AB)+vec(AC)+vec(AD)+vec(AE)+vec(AF) .
View SolutionIn a regular hexagon ABCDEF, prove that −−→AB+−−→AC+−−→AD+−−→AE+−−→AF=3−−→AD
04:19View SolutionConsider the regular hexagon ABCDEF with centre at O (origin). Five forces vec(AB), vec(AC), vec(AD), vec(AE), vec(AF) act at the vertex A of a regular hexagon ABCDEF. Then their resultant is
04:41View Solution

