ABCDEF is a regular hexagon with point O as centre. Find the value of −−→AB+−−→AC+−−→AD+−−→AE+−−→AF.
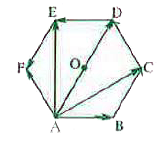
From the diagram
(−−→AB=−−−→DE)(−−→BC=−−−→EF)
−−→AB+−−→AC+−−→AD+−−→AE+−−→AF
=cancelvec(AB)+(cancelvec(AB)+cancelvec(BC))+vec(AD)+(cancelvec(AD)+cancelvec(DE))+(vec(AD)+cancelvec(DE)+cancelvec(EF))
=3−−→AD=3(2−−→AO)=6(−−→AO)
Similar Questions
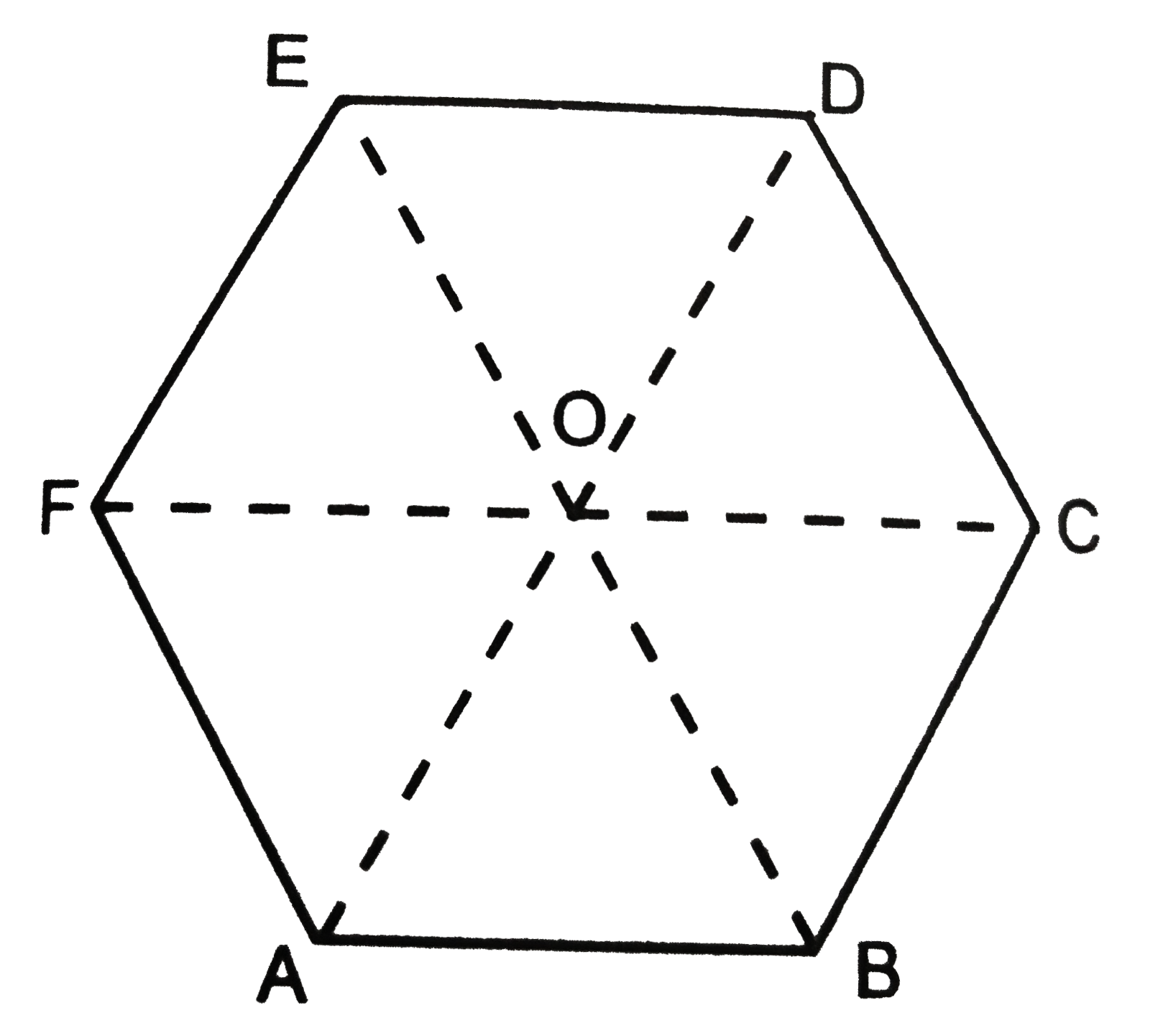
ABCDEF is a regular hexagon with point O as centre. The value of −−→AB+−−→AC+−−→AD+−−→AE+−−→AF is
View SolutionABCDEF is a regular hexagon, Fig. 2 (c ) .65. What is the value of
(−−→AB+−−→AC+−−→AD+−−→AE+−−→AF?
 .View Solution
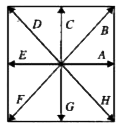
.View SolutionA number of vectors are as shown in .They can be combined in various ways , like →A+→C=→B . What is the value of (a) →E+→C (b) →A+→F (c ) →A+→D (d) →E+→A (e ) →A−→B .
 View Solution
View SolutionABCDEF is a regular hexagon with centre a the origin such that −−→AB+−−→EB+−−→FC=λ−−→ED then λ= (A) 2 (B) 4 (C) 6 (D) 3
View SolutionABCDEF is a regular hexagon with centre a the origin such that −−→AB+−−→EB+−−→FC=λ−−→EDthenλ= (A) 2 (B) 4 (C) 6 (D) 3
View SolutionIn Fig. ABCDEF is a ragular hexagon. Prove that
−−→AB+−−→AC+−−→AD+−−→AE+−−→AF=6−−→AO.View SolutionABCDEF is a regular hexagon. Find the vector →AB+→AC+→AD+→AE+→AF in terms of the vector →AD
View SolutionABCDEF is a regular hexagon. Find the vector →AB+→AC+→AD+→AE+→AF in terms of the vector →AD
View SolutionConsider the ragular hexagon ABCDEF with centre at O (origin).
Five forces −−→AB,−−→AC,−−→AD,−−→AE,−−→AF act at the vertex A of a regular hexagon ABCDEF. Then their resultant isView SolutionABCDEF be a regular hexagon in the xy-plane and −−→AB=4ˆi then →CD =
View Solution

