A cell of e.m.f. E is connected with an external resistance R , then p.d. across cell is V . The internal resistance of cell will be
(E−V)RE
(E−V)RV
(V−E)RV
(V−E)RE
The correct Answer is:B
V=E−ir
⇒V=E−(ER+r)r⇒V(R+r)=ER+Er−Er
⇒R(E−V)V
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ERRORLESSCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT BASED QUESTIONS (DIFFERENT MEASURING INSTRUMENTS)
74 Videos
- CURRENT ELECTRICITYBOOK - ERRORLESSCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT BASED QUESTIONS (HEATING EFFECT OF CURRENT)
67 Videos
- CURRENT ELECTRICITYBOOK - ERRORLESSCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT BASED QUESTIONS (Grouping of Resistances)
69 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - ERRORLESSCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Assertion and Reason
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - ERRORLESSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSERTION & REASON
20 Videos
Similar Questions
When a celll is connected to an external resistance R1, current through it is i1. When the same cell is connected to an external resistance R2, current through it is i2. Calculate the emf and internal resisance of the cell.
View SolutionThe maximum power dissipated in an external resistance R, when connected to a cell of emf E and internal resistance r, will be
View Solution
Knowledge Check
A cell of emf 1.5 Vis connected with an external resistance 2Ω. The potential difference falls to 1.0 v. The internal resistance of cell is
A1.5ΩB1.0ΩC10.0ΩD2.0ΩA cell of emf 1.5 Vis connected with an external resistance 2Ω. The potential difference falls to 1.0 v. The internal resistance of cell is
A1.5ΩB1.0ΩC10.0ΩD2.0ΩA cell of emf 1.5 V is connected with an external resistance 20Ω. The potential difference falls to 1.0 V. The internal resistance of cell is
A1.5ΩB1.0ΩC10.0ΩD2.0Ω
The emf of a cell is 2 V. When the terminals of the cell is connected to a resistance 4Ω. The potential difference across the terminals, if internal resistance of cell is 1Ω is
View SolutionTwo cells of same emf ε but of different internal resistances r1 and r2 are connected in series with an external resistance R. The potential drop across the first cell is found to be zero. The external resistance R is
View SolutionTwo cells of the same e.mf. e but different internal resistances r1andr2 are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris
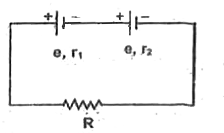
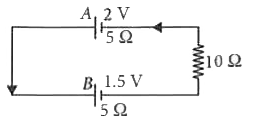
View SolutionTwo cells A and B of e.m.f.2 V and 1.5 V respectively, are connected as shown in figure through an external resistance 10 Ω The internal resistance of each cell is 5 Ω. The potential difference EAandEB across the terminals of the cells A and B respectively are
View SolutionIn a connection of 10 dry cells each of emf E and internal resistance r in series, two cell is connected opposite. Net emf and net internal resistance will be:
View Solution
