Two resistors of resistances 200kΩ and 1MΩ respectively form a potential divider with outer junctions maintained at potentials of + 3V and −15 V. Then, the potential at the junction between the resistors is-
+1V
−0.6V
0V
−12V
The correct Answer is:C
To solve the problem of finding the potential at the junction between two resistors in a potential divider, we can follow these steps:
Step 1: Identify the resistances and potentials
We have two resistors:
- R1=200kΩ=200×103Ω
- R2=1MΩ=1×106Ω
The outer potentials are:
- V1=+3V
- V2=−15V
Step 2: Calculate the equivalent resistance
Since the resistors are in series, the equivalent resistance Req is given by:
Req=R1+R2=200×103+1×106=1.2×106Ω
Step 3: Calculate the total voltage across the resistors
The total voltage Vtotal across the resistors is the difference between the two potentials:
Vtotal=V1−V2=3−(−15)=3+15=18V
Step 4: Calculate the current flowing through the circuit
Using Ohm's law, the current I flowing through the circuit can be calculated as:
I=VtotalReq=18V1.2×106Ω=15×10−6A=15μA
Step 5: Calculate the potential drop across R1
The potential drop VR1 across the resistor R1 can be calculated using Ohm's law:
VR1=I×R1=15×10−6×200×103=3V
Step 6: Calculate the potential at the junction
The potential at the junction Vx (between R1 and R2) can be found by subtracting the potential drop across R1 from the potential at the positive end:
Vx=V1−VR1=3V−3V=0V
Final Answer
The potential at the junction between the resistors is:
0V
We have two resistors:
- R1=200kΩ=200×103Ω
- R2=1MΩ=1×106Ω
- V1=+3V
- V2=−15V
Since the resistors are in series, the equivalent resistance Req is given by:
Req=R1+R2=200×103+1×106=1.2×106Ω
The total voltage Vtotal across the resistors is the difference between the two potentials:
Vtotal=V1−V2=3−(−15)=3+15=18V
Using Ohm's law, the current I flowing through the circuit can be calculated as:
I=VtotalReq=18V1.2×106Ω=15×10−6A=15μA
The potential drop VR1 across the resistor R1 can be calculated using Ohm's law:
VR1=I×R1=15×10−6×200×103=3V
The potential at the junction Vx (between R1 and R2) can be found by subtracting the potential drop across R1 from the potential at the positive end:
Vx=V1−VR1=3V−3V=0V
The potential at the junction between the resistors is:
0V
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ERRORLESSCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT BASED QUESTIONS (DIFFERENT MEASURING INSTRUMENTS)
74 Videos
- CURRENT ELECTRICITYBOOK - ERRORLESSCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT BASED QUESTIONS (HEATING EFFECT OF CURRENT)
67 Videos
- CURRENT ELECTRICITYBOOK - ERRORLESSCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT BASED QUESTIONS (Grouping of Resistances)
69 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - ERRORLESSCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Assertion and Reason
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - ERRORLESSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSERTION & REASON
20 Videos
Similar Questions
Two resistors of resistances 10Ω and 20Ω are joined in series. A potential difference of 12V is applied across the combination. Find the power consumed by each resistor.
View SolutionTwo resistors of resistances 10Ω and 20Ω are joined in parallel. A potential difference of 12V is applied across the combination. Find the power consumed by each resistor.
View Solution
Knowledge Check
Two resistors of resistances 200kΩand1Mω respectively form a potential divider with outer junctions maintained at potentials of +3Vand−15V. Then, the potential at the junction between the resistors is
A0VB+1VC−12VD+12VThe potential drop across the 3Ω resistor is
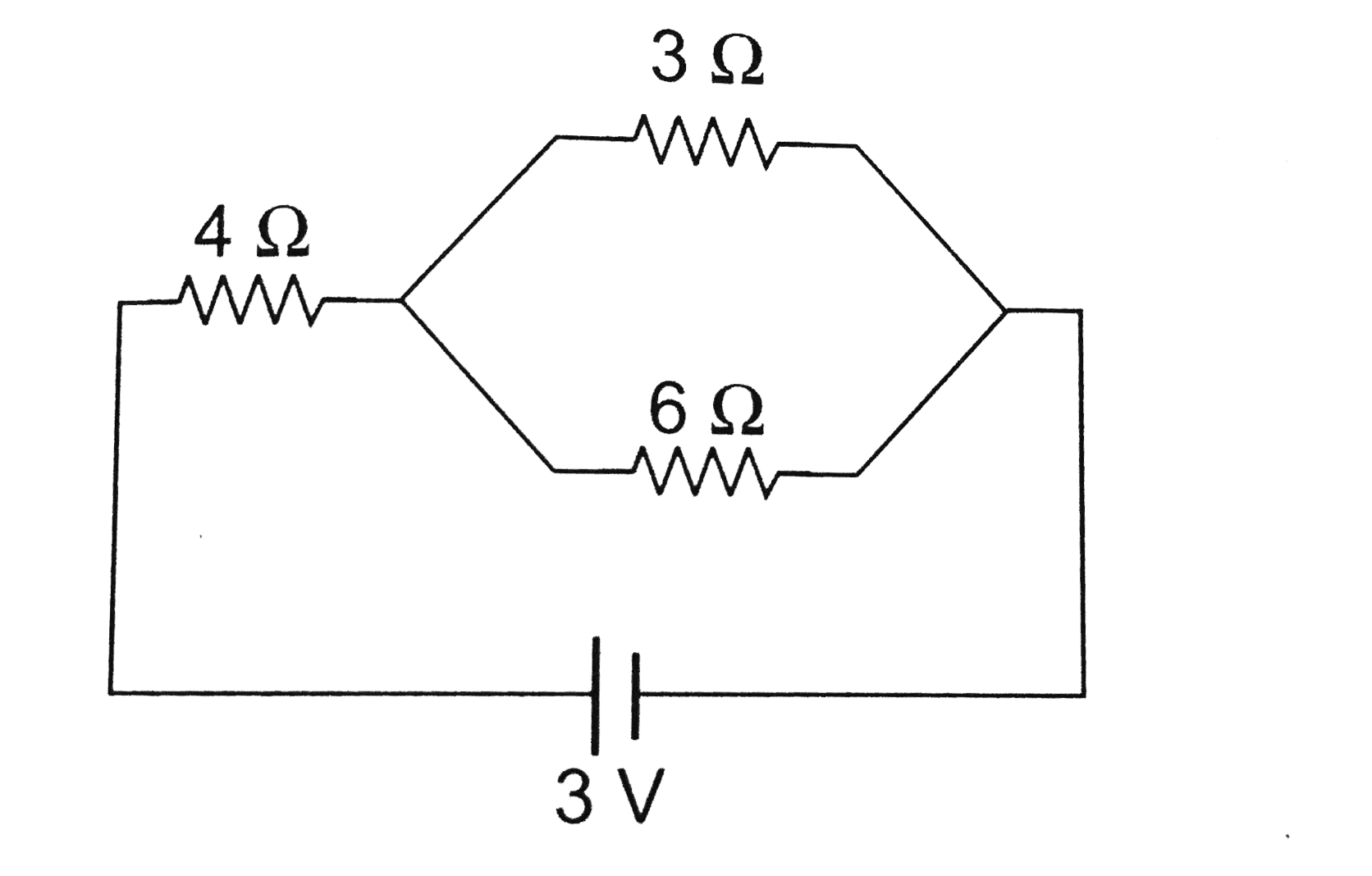 A1VB1.5VC2VD3V
A1VB1.5VC2VD3VIf two resistors of resistance 30Ω and 40Ω are con-nected in parallel across a battery, then the ratio of potential difference across them is ______.
A1:1B2:1C3:4D4:3
Two resistors X and Y of resistances 2 ω and 3 ω respectively are first joined in parallel and then in series. In each case the voltage supplied is 5 V.
(i) Draw circuit diagrams to show the combination of resistors in each case.
(ii) Calculate the voltage across the 3 Q resistor in the series combination of resistors.
View SolutionA voltmeter of resistance 600Ω is used to measure the potential drop across the 300Ω resistor. What will be the measured potential drop ?
View SolutionThree cells of emf 2.0 v, 1.8 V and 1.5 V are connected in series. Their internal resistances are 0.05Ω,0.7Ω and 1Ω respectively. If the battery is connected to an external resistor of 4Ω via a very resistance ammeter, what would be the reading in the ammeter ?
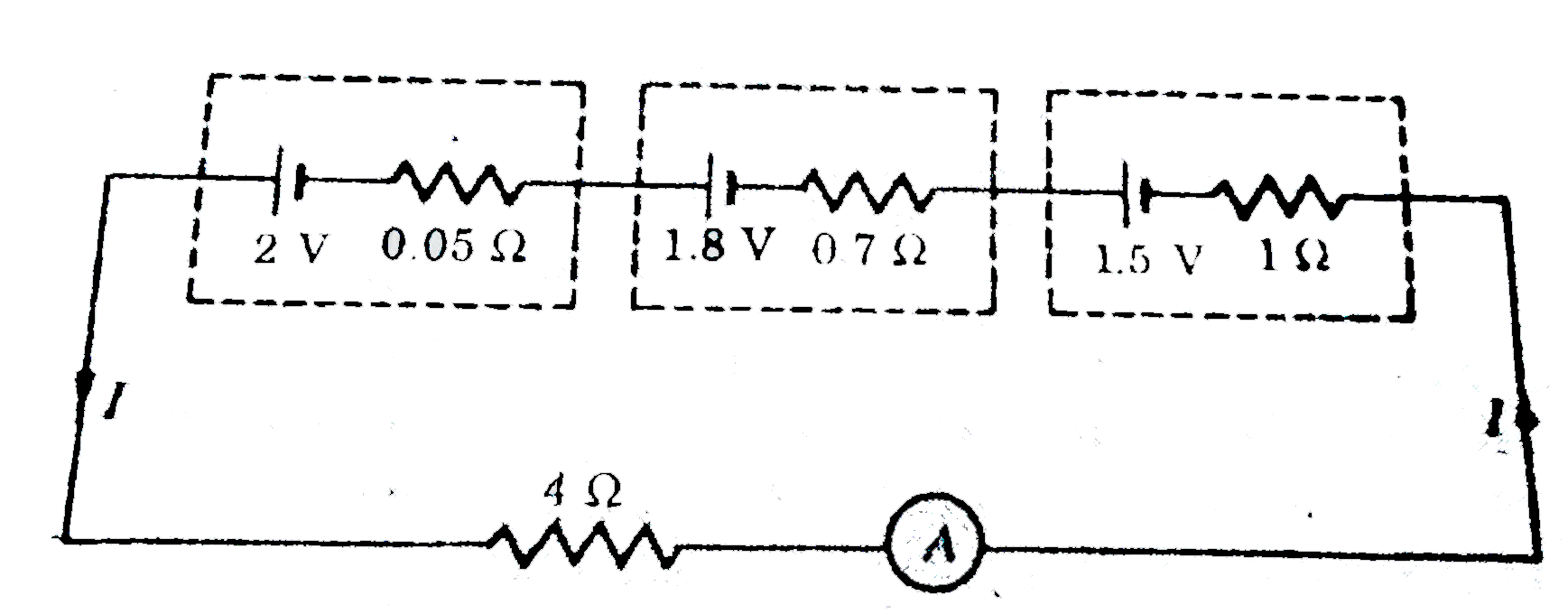
View SolutionThree resistors of resistance 2Ω,5Ω and 3Ω respectively are connected in parallel across a battery of 10 volts and negligible resistance. The potential difference across 5 Ω resistor is
View SolutionA 3Ω resistor and a 6Ω resistor are connected in parallel and the combination is connected in series to a battery of 5 V and a 3Ω resistor. The potential difference across the 6Ω resistor
View Solution
