A metallic rod of mass per unit length 0.5 kg m−1 is lying horizontally on a smooth inclined plane which makes an anlge of 30∘ with the horizontal. The rod is not allowed to slide down by flowing a current through it when a magnetic field of induction 0.25 T is acting on it in the vertical direction. The current flowing in the rod to keep it stationary
7.14 A
5.98 A
14.76 A
11.32 A
The correct Answer is:D

ilBcosθ=mgsinθ
i=mglBtanθ=(ml)gtanθB
i=0.5×9.80.25×1√3=11.3 amp.
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT BOOK - ERRORLESSCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - ASSERTION & REASON
18 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - ERRORLESSCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - NCERT BASED QUESTIONS (Force and Torque on a Current Carrying Conductor )
51 Videos
- ELECTROSTATICSBOOK - ERRORLESSCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION & REASON
25 Videos
- MAGNETISMBOOK - ERRORLESSCHAPTER - MAGNETISMEXERCISE - Assertion and Reason
22 Videos
Similar Questions
The figure shows a conductor of weight 1.0N& length L=0.5m placed on a rough inclined plane making an angle 30∘ with the horizontal so that conductor is perpendicular to a uniform horizontal magnetic field of induction B=0.10T.The coefficient of static friction betwen the conductor inside the plane of is 0.1A A current of l=10A flows through the conductor inside the plane of this paper as shown.What is the force needed to be applied parallel to the inclined plane to keep the conductor at rest?

View SolutionA rod of mass m, length l and resistance R is sliding down on a smooth inclined parallel rails with a cinstant velocity v. If a uniform horizontal magnetic field B exists, then find thevalue of B.
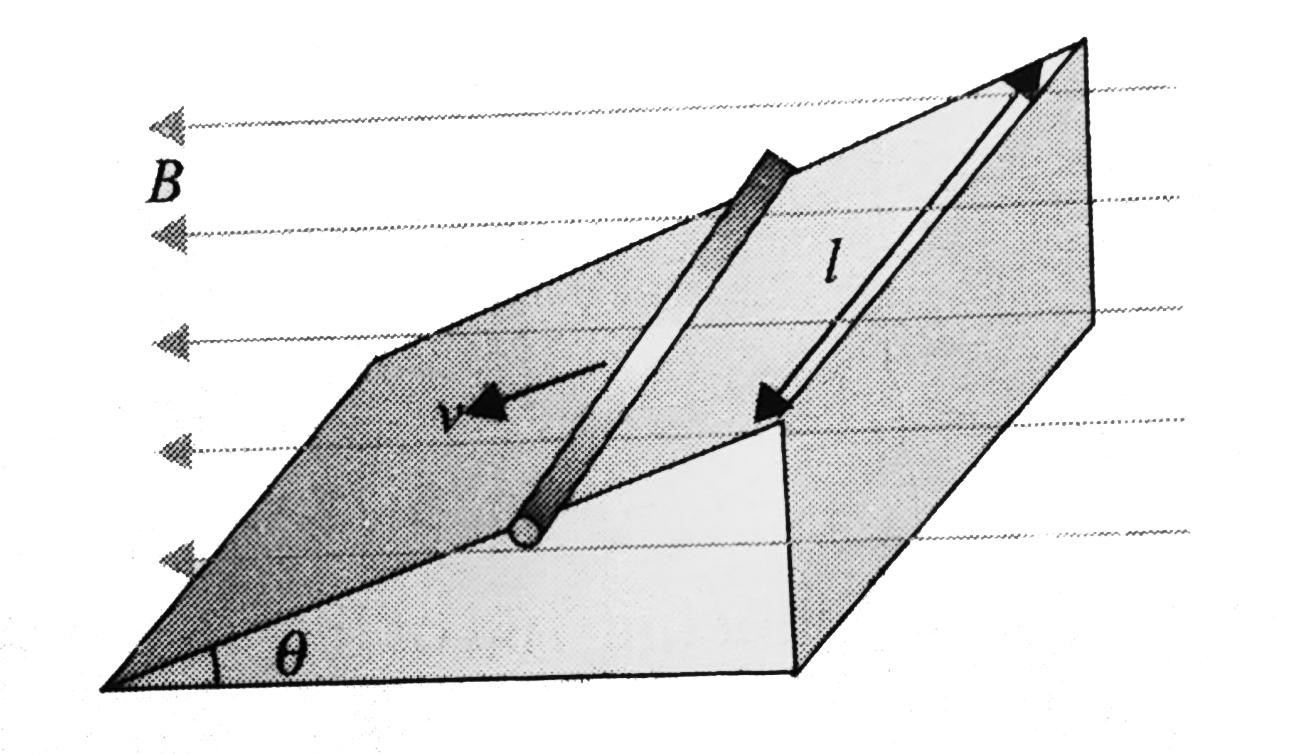
View Solution
Knowledge Check
A metallic rod of mass per unit length 0.5kgm−1 is lying horizontally on a straght inclined plane which makes an angle of 30∘ with the horizontal. The rod is not allowed to slide down by flowing a current throguh it when a magnetic field of induction 0.25T is acting on it in the vertical direction. The current flowing in the rod to keep it stationary is
A7.14AB5.98AC14.76AD11.32AA metallic rod of mass per unit length 0.5 kg m−1 is lying horizontally on a smooth inclined plane which makes an anlge of 30∘ with the horizontal. The rod is not allowed to slide down by flowing a current through it when a magnetic field of induction 0.25 T is acting on it in the vertical direction. The current flowing in the rod to keep it stationary
A14.76 AB5.98 AC7.14 AD11.32 AA horizontal rod of mass 10g and length 10cm is placed on a smooth plane inclined at an angle of 60∘ with the horizontal with the length of the rod parallel to the edge of the inclined plane. A uniform magnetic field induction B is applied vertically downwards. If the current through the rod is 1⋅73ampere, the value of B for which the rod remains stationary on the inclined plane is
A0⋅5TB1⋅0TC1⋅5TD1⋅7T
On a smooth inclined plane at 30∘ with the horizontal a thin current carrying metallic rod is placed parallel to the horizontal ground. The plane is located in a uniform magnetic field of 0⋅15tesla in the vertical direction. For what value of current can the rod ramain stationary? The mass per unit length of rod is 0⋅30kgm−1.
View SolutionA conductor (rod) of mass m, length l carrying a current i is subjected to a magnetic field of induction B. If the coefficients of friction between the conducting rod and rail is μ, find the value of I if the rod starts sliding.
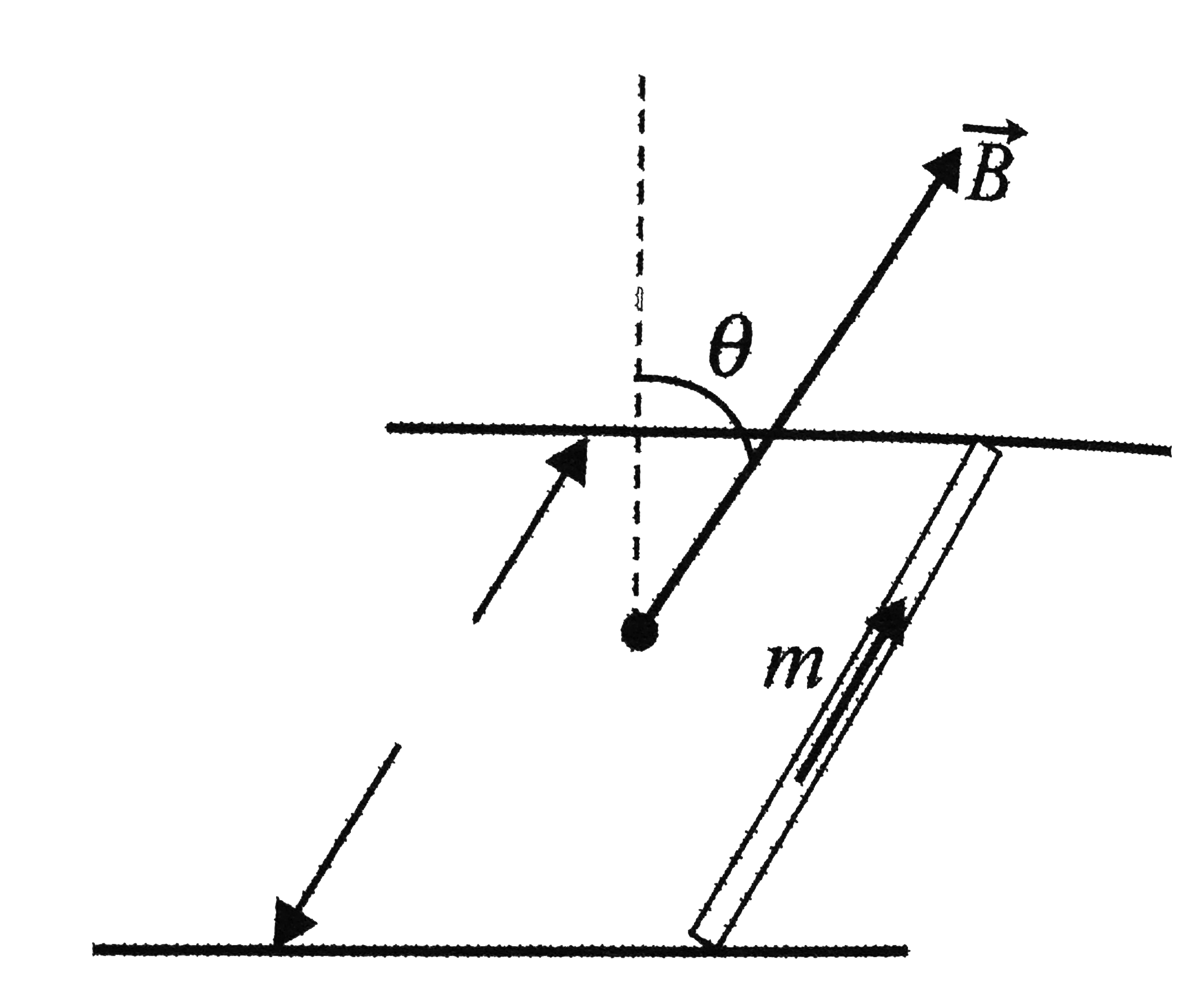
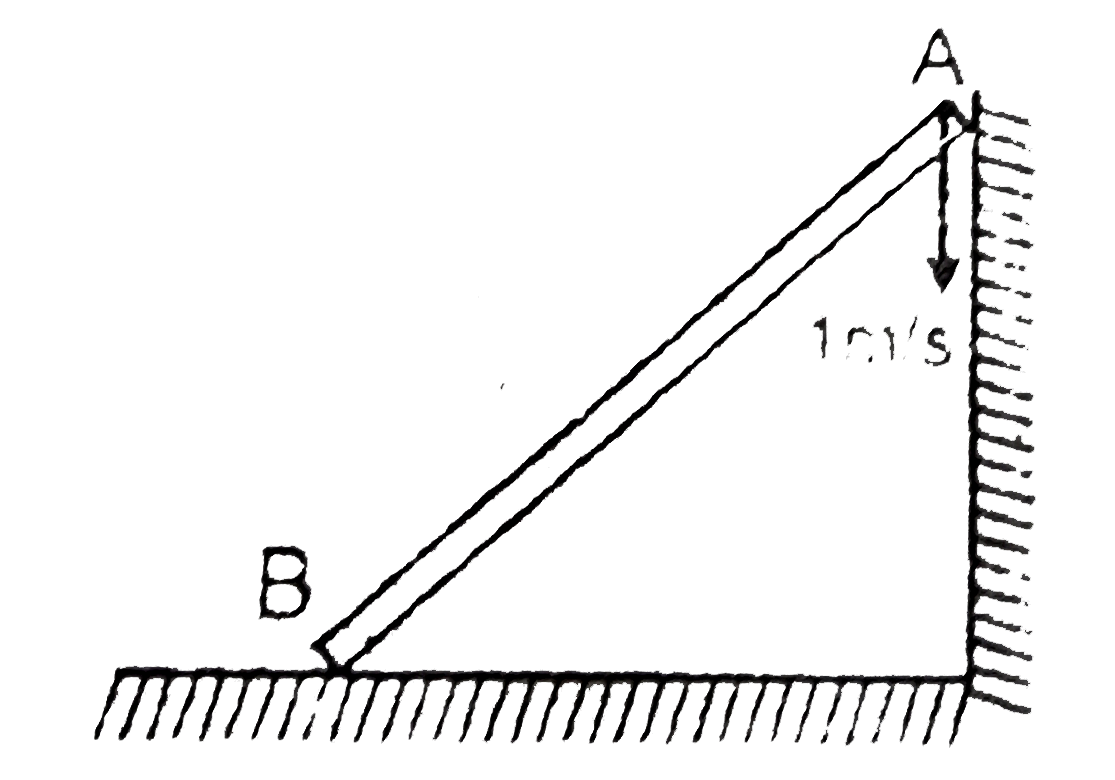
View SolutionA rod of length 1m is sliding in a corner as shown. At an instant when the rod makes an angle of 60∘ with the horizontal plane, the velocity of point A on the rod is 1 m/s. The angular velocity of the rod at this instant is :
View SolutionA rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:

View SolutionA current of 1 A flows a wire of length 0.1 m in a magnetic field of 0.5 T. The force acting on the wire when it makes an angle of 90∘ with the field is
View Solution
