Two spherical black bodies of radii r1 and r2 and with surface temperature T1 and T2 respectively radiate the same power. Then the ratio of r1 and r2 will be
(T2T1)2
(T2T1)4
(T1T2)2
(T1T2)4
The correct Answer is:A
To solve the problem, we need to find the ratio of the radii r1 and r2 of two spherical black bodies that radiate the same power. We will use the Stefan-Boltzmann law, which states that the power radiated by a black body is proportional to the fourth power of its absolute temperature and its surface area.
1. Understand the Power Radiated by a Black Body:
The power P radiated by a black body is given by the formula:
P=σAT4
where σ is the Stefan-Boltzmann constant, A is the surface area of the body, and T is the absolute temperature.
2. Surface Area of a Sphere:
The surface area A of a sphere with radius r is given by:
A=4πr2
3. Set Up the Power Equations for Both Bodies:
For the first body with radius r1 and temperature T1:
P1=σ(4πr21)T41
For the second body with radius r2 and temperature T2:
P2=σ(4πr22)T42
4. Equate the Powers:
Since both bodies radiate the same power, we have:
P1=P2
This leads to:
σ(4πr21)T41=σ(4πr22)T42
5. Cancel Common Terms:
We can cancel σ and 4π from both sides:
r21T41=r22T42
6. Rearrange the Equation:
Rearranging gives:
r21r22=T42T41
7. Take the Square Root:
Taking the square root of both sides:
r1r2=T22T21
8. Final Ratio:
Thus, the ratio of the radii r1 and r2 is:
r1r2=(T2T1)2
Conclusion:
The ratio of the radii r1 and r2 of the two spherical black bodies is given by:
r1r2=(T2T1)2
The power P radiated by a black body is given by the formula:
P=σAT4
where σ is the Stefan-Boltzmann constant, A is the surface area of the body, and T is the absolute temperature.
The surface area A of a sphere with radius r is given by:
A=4πr2
For the first body with radius r1 and temperature T1:
P1=σ(4πr21)T41
For the second body with radius r2 and temperature T2:
P2=σ(4πr22)T42
Since both bodies radiate the same power, we have:
P1=P2
This leads to:
σ(4πr21)T41=σ(4πr22)T42
We can cancel σ and 4π from both sides:
r21T41=r22T42
Rearranging gives:
r21r22=T42T41
Taking the square root of both sides:
r1r2=T22T21
Thus, the ratio of the radii r1 and r2 is:
r1r2=(T2T1)2
The ratio of the radii r1 and r2 of the two spherical black bodies is given by:
r1r2=(T2T1)2
Topper's Solved these Questions
- TRANSMISSION OF HEAT Book:ERRORLESSChapter:TRANSMISSION OF HEAT Exercise:NCERT BASED QUESTIONS (Radiation (Newton.s Law of Cooling))
Explore 11 Videos
- TRANSMISSION OF HEAT Book:ERRORLESSChapter:TRANSMISSION OF HEAT Exercise:PAST YEARS QUESTIONS
Explore 21 Videos
- TRANSMISSION OF HEAT Book:ERRORLESSChapter:TRANSMISSION OF HEAT Exercise:NCERT BASED QUESTIONS (Radiation (Wien.s law))
Explore 13 Videos
- THERMOMETRY, THERMAL EXPANSION AND CALORIMETRYBook:ERRORLESSChapter:THERMOMETRY, THERMAL EXPANSION AND CALORIMETRYExercise:ASSERTION & REASON
Explore 10 Videos
- UNITS, DIMENSIONS AND MEASUREMENTBook:ERRORLESSChapter:UNITS, DIMENSIONS AND MEASUREMENTExercise:ASSERTION & REASON
Explore 17 Videos
Similar Questions
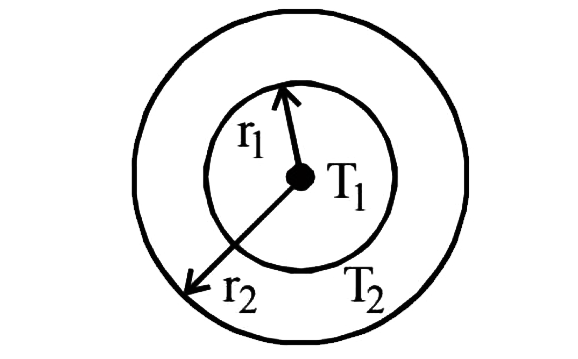
Fig, shows a system of two concentric spheres of radii r1 andr2 and kept at temperature T1 and T2(T1>T2) respectively. Find the expression for radial rate of flow of heat through the substance.

View SolutionTwo wires of same material and same length have radii r1andr2 respectively. Compare their resistances.
View Solution
Knowledge Check
Two spherical black bodies of radii R1 and R2 and with surface temperature T1 and T2 respectively radiate the same power. R1/R2 must be equal to
A(T1T2)2B(T2T1)2C(T1T2)4D(T2T1)4The figure shows a system of two concentric spheres of radii r1andr2 are kept at temperature T1andT2, respectively. The radial rate of flow of heat in a substance between the two concentric spheres is proportional to
 AIn(r2r1)Br2−r1r1r2C(r1−r2)Dr1r2r2−r1
AIn(r2r1)Br2−r1r1r2C(r1−r2)Dr1r2r2−r1Two spheres of the same material having radii r and 4r and temperature 2T0 and T0 respectively. The ratio of rate of radiation of energy by the sphere is
A1:1B1:2C2:1D3:1
Two charged spherical conductors of radii R1andR2 when connected by a connecting wire acquire charges q1andq2 respectively. Find the ratio of their charge densities in terms of their radil ?
View SolutionTwo planets have radii r1and2r1 and densities are ρ1and4ρ1 respectively. The ratio of their acceleration due to gravities is
View SolutionTwo planets have radii r1andr2 and densities d1andd2 respectively. Then the ratio of acceleration due to gravity on them is
View SolutionTwo spheres of radii R1 and R2 are made of the same material and are at the same temperature. The ratio of their thermal capacities is:
View SolutionA spherical black body of radius r radiated power P at temperature T when placed in surroundings at temprature T0(<<T) If R is the rate of colling .
View Solution
