A hollow copper sphere S and a hollow copper cube C, both of negligible thin walls of same area, are filled with water at 90°C and allowed to cool in the same environment. The graph that correctly represents their cooling is
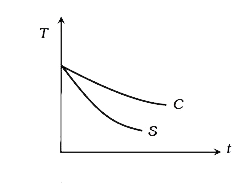
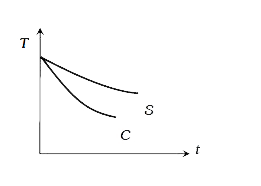
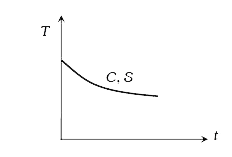
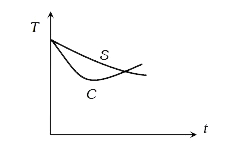
The correct Answer is:C
As dθdt=εAσmc4θ3Δθ
For given sphere and cube εAσmc4θ3Δθ is constant dθdt = constant.
Topper's Solved these Questions
- TRANSMISSION OF HEAT BOOK - ERRORLESSCHAPTER - TRANSMISSION OF HEAT EXERCISE - NCERT BASED QUESTIONS (Radiation (Newton.s Law of Cooling))
11 Videos
- TRANSMISSION OF HEAT BOOK - ERRORLESSCHAPTER - TRANSMISSION OF HEAT EXERCISE - PAST YEARS QUESTIONS
21 Videos
- TRANSMISSION OF HEAT BOOK - ERRORLESSCHAPTER - TRANSMISSION OF HEAT EXERCISE - NCERT BASED QUESTIONS (Radiation (Wien.s law))
13 Videos
- THERMOMETRY, THERMAL EXPANSION AND CALORIMETRYBOOK - ERRORLESSCHAPTER - THERMOMETRY, THERMAL EXPANSION AND CALORIMETRYEXERCISE - ASSERTION & REASON
10 Videos
- UNITS, DIMENSIONS AND MEASUREMENTBOOK - ERRORLESSCHAPTER - UNITS, DIMENSIONS AND MEASUREMENTEXERCISE - ASSERTION & REASON
17 Videos
Similar Questions
A solid sphere of copper of radius R and a hollow sphere of the same materail of inner radius r and outer radius A are heated to the same temperature and allowed to cool in the same environment. Which of tehm starts cooling faster?
View SolutionA solid sphere of radius R and a hollow sphere of inner radius R/2 and outer radius R, made of copper ,are heated to the same temperature and are allowed to cool in the same environment .Then
View Solution
Knowledge Check
A solid sphere of copper of radius R and hollow sphere of copper of inner radius r and outer radius R are heated to the same temperature and allowed to cool in the same environment. The rate of cooling is
Amore for hollow sphereBmore for solid sphereCsame for both the sphereDcan not sayAssertion : A solid sphere of copper of radius R and a hollow sphere of the same material of inner radius r and outer radius R are heated to the same temperature and allowed to cool in the same environment. The hollow sphere cools faster.
Reason : Rate of cooling is according to Stefan's law which is EαT4AIf both assertion and reason are true and reason is the correct explanation of assertionBIf the assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.A hollow copper sphere & a hollow copper cube of same surface area & negligible thickness , are filled with warm water of same temperature and placed in an enclosure of constant temperature a few degrees below that of the bodies. Then in the beginning:-
AThe rate of energy lost by the sphere is greater than that by the cubeBThe rate of energy lost by the two are equalCThe rate of energy lost by the sphere is less than that by the cubeDThe rate of fall of temperature for sphere is less than that for the cube
A solid sphere and a hollow sphere of the same material and size are heated to the same temperature and allowed to cool in the same surroundings. If the temperature difference between the surroundings and each sphere is T, then :
View SolutionA sphere and a cube of same material and same volume are heated up to same temperature and allowed to cool in the same sorroundings. The radio of the amounts of radiations emitted in equal time intervals will be
View SolutionA hollow copper sphere & a hollow copper cube of same surface area & negligible thickness , are filled with warm water of same temperature and placed in an enclosure of constant temperature a few degrees below that of the bodies. Then in the beginning:-
View SolutionAssertion : A solid sphere and a hollow sphere of same material and same radius are kept at same temperature in atmosphere. Rate of cooling of hollow sphere will be more.
Reason : If all other conditions are same, then rate of cooling is inversely proportional to the mass of body.
View SolutionA solid sphere, a cube and a plate, all are made of same material and all have same mass. These are heated to a temperature 100∘C and then allowed to cool at the temperature of room. Which of these will cool down first –
View Solution
