A particle of mass M and charge q is released from rest in a region of uniform electric field of magnitude E. After a time t, the distance travelled by the charge is S and the kinetic energy attained by the particle is T. Then, the ratio T/S
Remains constant with time t
Varies linearly with the mass M of the particle
Is independent of the charge q
Is independent of the magnitude of the electric field E
The correct Answer is:A
To solve the problem, we need to find the ratio of the kinetic energy T attained by a particle of mass M and charge q after a time t to the distance S traveled by the particle in a uniform electric field of magnitude E.
1. Determine the Force on the Particle:
The force F acting on the charged particle in an electric field E is given by:
F=qE
2. Apply Newton's Second Law:
According to Newton's second law, the acceleration a of the particle can be expressed as:
F=Ma⟹a=FM=qEM
3. Calculate the Distance Traveled (S):
Since the particle is released from rest, we can use the equation of motion:
S=ut+12at2
where u=0 (initial velocity). Thus, we have:
S=12at2=12(qEM)t2
Simplifying this gives:
S=qEt22M
4. Calculate the Kinetic Energy (T):
The kinetic energy T of the particle after time t is given by:
T=12Mv2
To find v, we use the equation:
v=u+at=0+(qEM)t=qEtM
Now substituting v into the kinetic energy formula:
T=12M(qEtM)2=12M⋅q2E2t2M2=q2E2t22M
5. Find the Ratio TS:
Now, we can find the ratio of kinetic energy T to distance S:
TS=q2E2t22MqEt22M=q2E2t22M⋅2MqEt2
Simplifying this gives:
TS=qE1=qE
Final Answer:
The ratio TS is:
TS=qE
The force F acting on the charged particle in an electric field E is given by:
F=qE
According to Newton's second law, the acceleration a of the particle can be expressed as:
F=Ma⟹a=FM=qEM
Since the particle is released from rest, we can use the equation of motion:
S=ut+12at2
where u=0 (initial velocity). Thus, we have:
S=12at2=12(qEM)t2
Simplifying this gives:
S=qEt22M
The kinetic energy T of the particle after time t is given by:
T=12Mv2
To find v, we use the equation:
v=u+at=0+(qEM)t=qEtM
Now substituting v into the kinetic energy formula:
T=12M(qEtM)2=12M⋅q2E2t2M2=q2E2t22M
Now, we can find the ratio of kinetic energy T to distance S:
TS=q2E2t22MqEt22M=q2E2t22M⋅2MqEt2
Simplifying this gives:
TS=qE1=qE
The ratio TS is:
TS=qE
Topper's Solved these Questions
- ELECTROSTATICSBOOK - ERRORLESSCHAPTER - ELECTROSTATICSEXERCISE - NCERT BASED QUESTIONS (Electric Dipole)
21 Videos
- ELECTROSTATICSBOOK - ERRORLESSCHAPTER - ELECTROSTATICSEXERCISE - NCERT BASED QUESTIONS (Electric Flux and Gauss.s Law)
27 Videos
- ELECTROSTATICSBOOK - ERRORLESSCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION & REASON
25 Videos
- ELECTRONICSBOOK - ERRORLESSCHAPTER - ELECTRONICSEXERCISE - Assertion & Reason
26 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - ERRORLESSCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - ASSERTION & REASON
18 Videos
Similar Questions
A protons of mass m charge 2 e is released from rest in a uniform electric field of strength E .The time taken by it to travel a distance d in the field is..
View SolutionA particle of mass m and charge q is released from rest in uniform electric field of intensity E. Calculate the kinetic energy it attains afect moving a distance x between the plates.
View Solution
Knowledge Check
A charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :
A B
B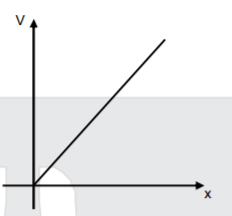 C
C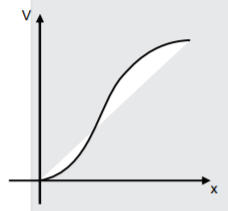 D
D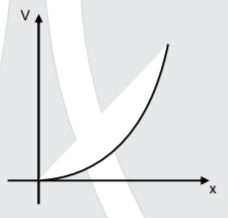
A charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
A2E2t2mqBE2q2r22mCEq2m2t2DEqm2tA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
A2E2t2mqBE2q2t22mCEq2m2t2DEqm2t
A protons of mass m charge c is released form rest in a uniform electric field of strength E .The time taken by it to travel a distance d in the field is
View SolutionAn electron of mass m and charge q is accelerated from rest in a uniform electric field of strength E the velocity acquired by it as it travels a distance l is
View SolutionAn electron of mass m and charge q is accelerated from rest in a uniform electric field of strength E. The velocity acquired by it as it travels a distance l is
View SolutionA particle of mass m and charge q is placed at rest in a uniform electric field E and then released, the kinetic energy attained by the particle after moving a distance y will be
View SolutionA charged particle of mass m and charge e is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is Ek and the linear momentum is p. We have
View Solution
