A smaller cube with side b (depicted by dashed lines) is excised from a bigger uniform cube with side a as shown below such that both cubes have a common vertex P. Let X = a/b. If the centre of mass of the remaining solid is at the vertex O of smaller cube then X satisfies.

x3−x2−x−1=0
x2−x−1=0
x3+x2−x−1=0
x3−x2−x+1=0
The correct Answer is:A
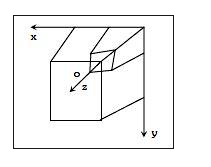
XCM=ρ(a3)(a2)−ρ(b3)(b2)ρ(a3)−ρ(b3)
We will consider removed mass as a negative mass
b=ρ(a42)−ρ(b42)ρ(a3)−ρ(b3)
a3b−b4=a42−b42
2a3b−2b4=a4−b4
Put a=bx
2b4x3−2b4=b4x4−b4
2x3−1=x4
2x3−2+1=x4
2(x3−1)=(x2+1)(x2−1)
2(x−1)(x2+1+x)=(x−1)(x+1)(x2+1)
2x2+2+2x=x3+x+x2+1
x3−x2−x−1=0
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Angular Displacement, Velocity and Acceleration)
34 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Moment of Inertia)
139 Videos
- NEWTON'S LAWS OF MOTIONBOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - ASSERTION & REASON
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assertion & Reason
15 Videos
Similar Questions
A square of side 4m having uniform thickness is divided into four equal squares as shown in Fig. If one of the squares is cut off, find

the position of centre of mass of the remaining portion from the centre O.
View SolutionA solid sphere of radius R is placed on a cube of side 2R. Both are made of same material. Find the distance of their centre of mass fro the interface.
View Solution
Knowledge Check
In the figure shown a semicircular area is removed from a uniform square plate of side l and mass ‘m’ (before removing). The x-coordinate of centre of mass of remaining portion is (The origin is at the centre of square)
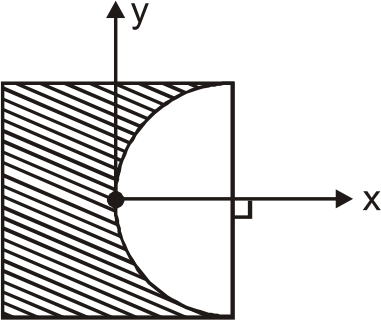 A−π(π−2)l2(8−π)Bπ(π−2)l2(8−π)C−π(π−2)l8−πD−l(π−43)2(8−π)
A−π(π−2)l2(8−π)Bπ(π−2)l2(8−π)C−π(π−2)l8−πD−l(π−43)2(8−π)Eight solid uniform cubes of edge l are stacked together to form a single cube with centre O. One cube is removed from this system. Distance, of the centre of mass of remaining 7 cubes from O is.
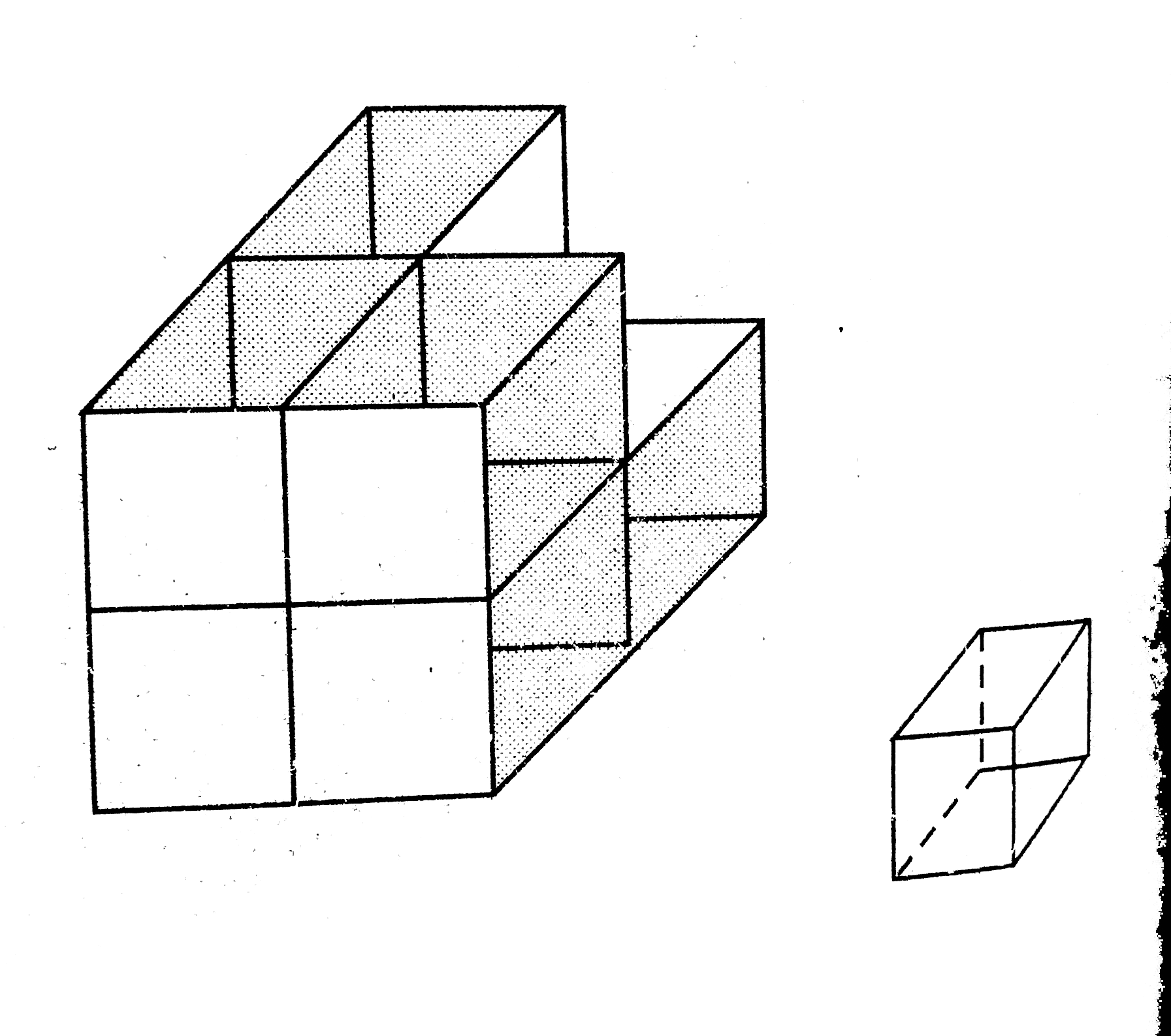 .A7√3l16B√3l16C√3l14Dzero
.A7√3l16B√3l16C√3l14DzeroA uniform circular disc of radius a is taken. A circular portion of radius b has been removed from it as shown in the figure. If the center of hole is at a distance c from the center of the disc, the distance x2 of the center of mass of the remaining part from the initial center of mass O is given by
 Aπb2(a2−b2)B−cb2(a2−b2)Cπc2(a2−b2)Dπa2(c2−b2)
Aπb2(a2−b2)B−cb2(a2−b2)Cπc2(a2−b2)Dπa2(c2−b2)
(i) A non uniform cube of side length a is kept inside a container as shown in the figure. The average density of the material of the cube is 2 ρ where ρ is the density of water. Water is gradually fille din the container. It is observed that the cube begins to topple, about its edge into the plane of the figure passing through pointA, when the height of the water in the container becomes a2. Find the distance of the centre of mass of the cube from the face AB of the cube. Assume that water seeps under the cube.
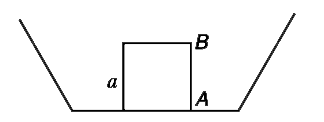
(ii) A rectangular concrete block (specific gravity =2.5) is used as a retatining wall in a reservoir of water. The height and width of the block are x and y respectively the height of water in the reservoir is z=34x. the concrete block cannot slide on the horizontal base but can rotate about an axis perpendicular to the plane of the figure and passing through point A
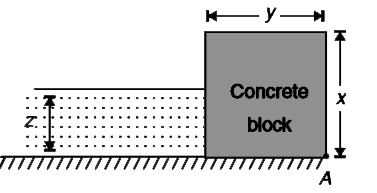
(a) Calculate the minimum value of the ratio yx for which the block will not begin to overturn about A.
(b) Redo the above problem for the case when there is a seepage and a thin film of water is present under the block. Assume that a seal at A prevents the water from flowing out underneath the block.
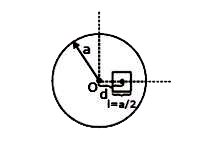
View SolutionA square shaped hole of side l=a2 is carved out at a distance d=a2 from the centre 'O' of a uniform circular disk of radius a. If the distance of the centre of mass of the remaining portion from O is −ax value of X (to the nearest integer) is _________.
View Solutionlet the point B be the reflection of the point A(2,3) with respect to the line 8x-6y-23=0. let TA and TB be circles of radii 2 and 1 with centres A and B respectively. Let T be a common tangent to the circles TA and TB such that both the circles are on the same side of T. if C is the point of intersection of T and the line passing through A and B then the length of the line segment AC is
View SolutionA solid cube of side 'a' is shown in the figure. Find maximum value of 100ba for which the block does not topple before sliding.

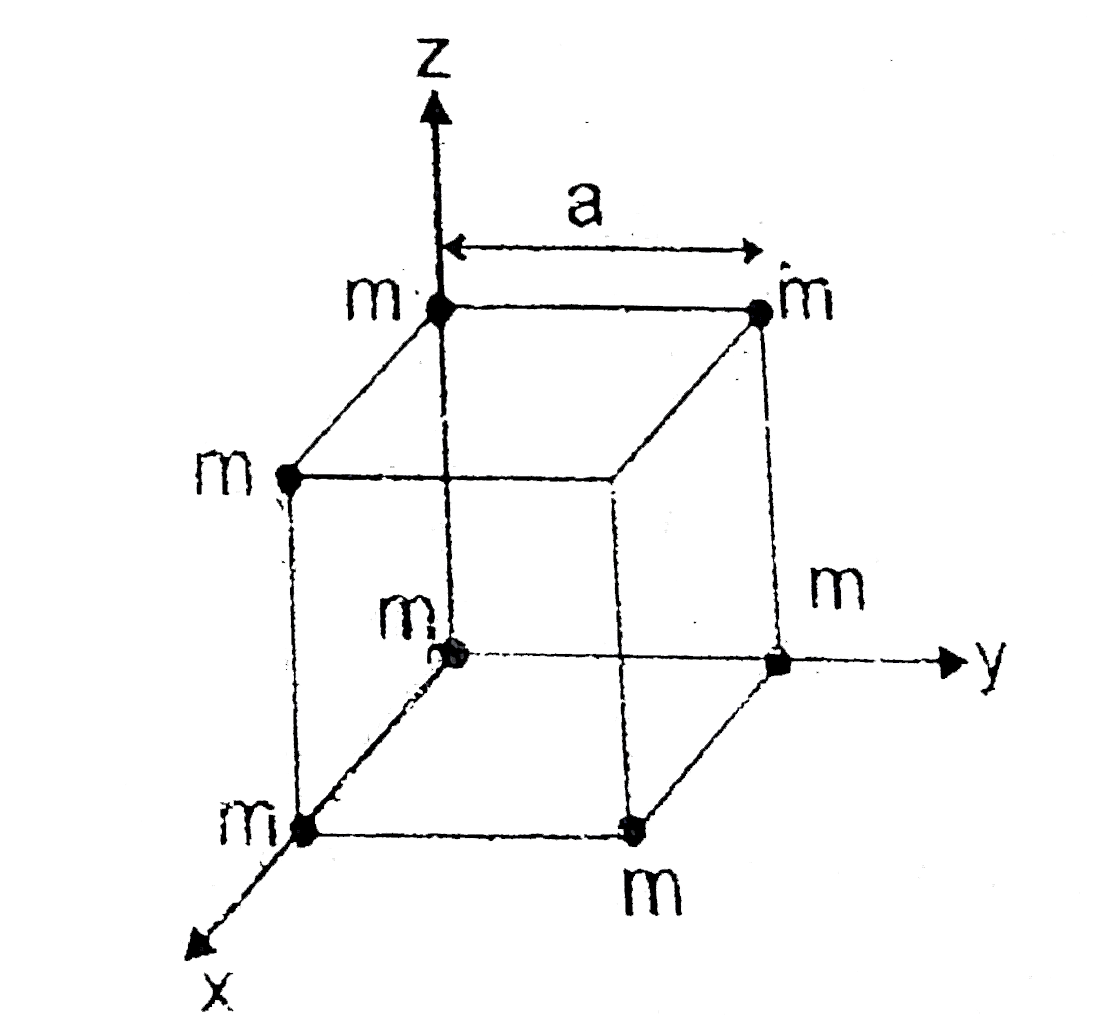
View SolutionSeven particles, each of mass m are placed at the seven corners of a cube of side 'a', but one corner is vacant, as shown in figure. If the x−coordinates of the centre of mass of the system is nam. Where n and m are least integer values. Then find vlaue of m−n.
View Solution
