A spherical cavity of radius r is carved out of a uniform solid sphere of radius R as shown in the figure. The distance of the center of mass of the resulting body from that of the solid sphere is given by
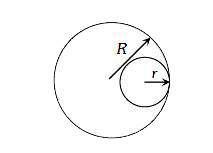
R−r2
0
R+r2
−r3R2+Rr+r3
The correct Answer is:D
X=−mR3r3(R−r)m−mr3R3
−mr3(R−r)m(R3−r3)
= −mr3(R−r)m(R−r)(R2+Rr+r2)=−r3R2+Rr+r3
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Angular Displacement, Velocity and Acceleration)
34 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Moment of Inertia)
139 Videos
- NEWTON'S LAWS OF MOTIONBOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - ASSERTION & REASON
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assertion & Reason
15 Videos
Similar Questions
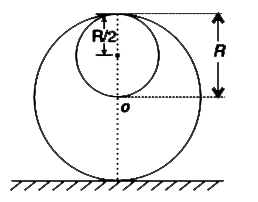
A spherical cavity of radiusR2 is removed from a solid sphere of radius R as shown in fig. The sphere is placed on a rough horizontal surface as shown. The sphere is given a gentle push. Friction is large enough to prevent slippage. Prove that the sphere perform SHM and find the time period.
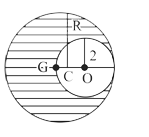
View SolutionAs shown in figure, when a spherical cavity (centered at O) of radius 2 is cut out of a uniform sphere of radius R (centered at C), the centre of mass of remaining (shaded) part of sphere is at G, i.e, on the surface of the cavity. R can be determined by the equation:
View Solution
Knowledge Check
A hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . Then y -coordinate of the centre of mass of the remaining sphere is
AYCM=−R15BYCM=−R40CYCM=−R30DYCM=−R20A hemi-spherical cavity is created in solid sphere (of radius 2R) as shown in the figure. Then
Axcm=−R/15Bycm=−R40Czcm=zeroDNone of these_E01_017_Q01.png)
A spherical cave of radius R/2 was carved out from a uniform sphere of radius R and original mass M. the center of the cave is at R/2 from the center of the large sphere. Point P is at a distance 2R from the center the large sphere and on the joing line of the two centers. the gravitational field strength g at point P isAg=GM4R2Bg=5GM8R2Cg=3GM16R2Dg=7GM36R2
The radius of gyration of a solid sphere of radius r about a certain axis is r. The distance of this axis from the centre of the sphere is
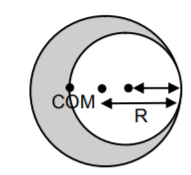
View SolutionA uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then
View SolutionThe radius of gyration of a solid sphere of radius R about its tangential is
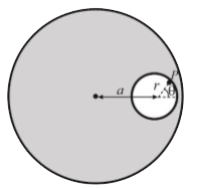
View SolutionA solid non-conducting sphere of radius R is charged with a uniform volume charge density ρ. Inside the sphere a cavity of radius r is made as shown in the figure. The distance between the centres of the sphere and the cavity is a. An electron of charge 'e' and mass 'm' is kept at point P inside the cavity at angle θ=45∘ as shown. If at t = 0 this electron is released from point P, calculate the time it will take to touch the sphere on inner wall of cavity again.
View SolutionThe radius of gyration of a uniform solid sphere of radius R., about an axis passing through a point R2 away from the centre of the sphere is:
View Solution