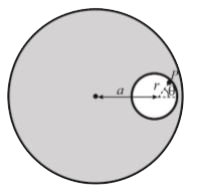
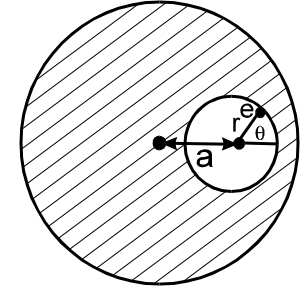
A solid non-conducting sphere of radius R is charged with a uniform volume charge density ρ. Inside the sphere a cavity of radius r is made as shown in the figure. The distance between the centres of the sphere and the cavity is a. An electron of charge 'e' and mass 'm' is kept at point P inside the cavity at angle θ=45∘ as shown. If at t = 0 this electron is released from point P, calculate the time it will take to touch the sphere on inner wall of cavity again.
√3Rmε0reρa
√6mε0reρa
√6√3mε0Reρa
√6√2mε0reρa
The correct Answer is:D
The magnitude of electric field inside the cavity Ecavity=ρa3∈0. It is directed along a in radially outward direction
For touching the sphere again, electron must move a distance 2rcos45∘ and time taken by electron for this is given as
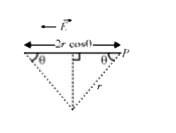
t=√2la
⇒
⎷2(√2r)eE/m
⇒t=
⎷6(√2mr∈0)eρa
Similar Questions
A solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

View SolutionA cavity of radius r is present inside a solid dielectric sphere of radius R, having a volume charge density of ρ. The distance between the centres of the sphere and the cavity is a. An electron e is kept inside the cavity at an angle θ=45∘ as shown. the electron (mass m and -e) touches the sphere again after time (P√2mrε0eaρ)1/2 ? Find the value of P. Neglect gravity.

View Solution
Knowledge Check
A hemi-spherical cavity is created in solid sphere (of radius 2R) as shown in the figure. Then
 Axcm=−R/15Bycm=−R40Czcm=zeroDNone of these
Axcm=−R/15Bycm=−R40Czcm=zeroDNone of theseA solid sphere having radius R and uniform charge density ρ has a cavity of radius R2 as shown in figure.Find the value of ∣∣∣EAEB∣∣∣
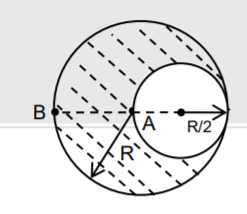 A1819B1117C917D919
A1819B1117C917D919A positively charge sphere of radius r0 carries a volume charge density ρ. A spherical cavity of radius r0/2 is then scooped out and left empty. C1 is the center of the sphere and C2 that of the cavity. What is the direction and magnitude of the electric field at point B?
 A17ρr054ε0leftBρr06ε0 leftC17ρr054ε0rightDρr06ε0right
A17ρr054ε0leftBρr06ε0 leftC17ρr054ε0rightDρr06ε0right
A thick shell with inner radius R and outer radius 3R has a uniform charge density rho.It has a spherical cavity of radius R as shown in figure.The electric field at the centre of the cavity is nρR12ɛ0. Find n.
View SolutionA cavity of radius r is present inside a fixed solid dielectric sphere of radius R, having a volume charge density of ρ. The distance between the centres of the sphere and the cavity is a. An electron is released inside the cavity at an angle θ=450 as shown. The electron (of mass m and charge –e) will take (P√2mrε0eaρ)1/2 time to touc the sphere again. Neglect gravity. find the value of P:
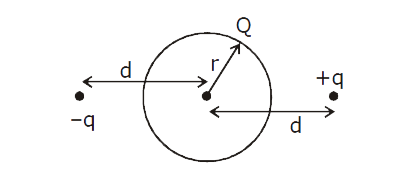
View SolutionA solid conducting sphere of radius r is having a charge Q and point charges +q and -q are kept at distance d from the centre of sphere as shown in the figure. The electric potential at the centre of solid sphere
(assume potential to be 0 at infinity)
View SolutionA nonconducting sphere of radius R is filled with uniform volume charge density −ρ. The center of this sphere is displaced from the origin by →d. The electric field →E at any point P having position vector inside the sphere is

View SolutionThere is a solid non-conducting sphere of radius R. Sphere is uniformly charged over the volume. Electric field due to this where in observed.
View Solution
