A ball is rolling without slipping in a spherical shallow bowl (radius R) as shown in the figure and is executing simple harmonic motion. If the radius of the ball is doubled, the period of oscillation

Increases slightly
Is reduced by a factor of 1/2
Is increased by a factor of 2
Decreases slightly
The correct Answer is:D
mgsinθ−Fr=ma
Fr=25mr2ar2⇒a=5gsinθ7R−r⇒ω=√5g7(R−r)
⇒T=2π√7(R−r)5r
Topper's Solved these Questions
- BOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - PAST YEARS QUESTIONS70videos
ROTATIONAL MOTION
- BOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - ASSERTION AND REASON25videos
ROTATIONAL MOTION
- BOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Work, Energy and Power)44videos
ROTATIONAL MOTION
- BOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - ASSERTION & REASON18videos
NEWTON'S LAWS OF MOTION
- BOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assertion & Reason15videos
SIMPLE HARMONIC MOTION
Similar Questions
The plot of velocity (v) versus displacement (x) of a particle executing simple harmonic motion is shown in figure. The time period of oscillation of particle is :-
 View Solution
View SolutionThe acceleration-displacement graph of a particle executing simple harmonic motion is shown in the figure. The frequency of oscillation is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The maximum velocity a particle, executing simple harmonic motion with an amplitude 7 mm, 4.4 m//s. The period of oscillation is.
A(a) 0.01sB(b) 10sC(c ) 0.1sD(d) 100s - Question 2 - Select One

A cylinder of radius R is to roll without slippoing between two planks as shown in the figure. ThenAangular velocity of the cylinder is vR counter clockwiseBangular velocity of the cylinder is 2vR clockwiseCvelocity of centre of mass of the cylinder is v towards leftDvelocity of centre of mass of the cylinder is 2v towards right. - Question 3 - Select One
A ball rolls without slipping. The radius of gyration of the ball about an axis passing through its centre of mass is k. If radius of the ball be R, then the fraction of total energy associated with its rotation will be.
Ak2+R2R2Bk2R2Ck2k2+R2DR2k2+R2
The acceleration-displacement (a−X) graph of a particle executing simple harmonic motion is shown in the figure. Find the frequency of oscillation.
 View Solution
View SolutionWhat is the work done in upturning a thin hemispherical bowl as shown in the figure. The mass of the bowl is M and the radius of the bowl is R.
View SolutionA small sphere S of radius ,r and mass m rolls without slipping, inside a large hemispherical bowl B of radius R as shown in figure. S starts from rest at the top point of the hemisphere
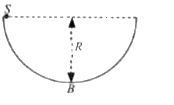 View Solution
View SolutionA particle executes simple harmonic motion according to equation 4d2xdt2+320x=0. Its time period of oscillation is :-
View SolutionThe acceleration displacement graph of a particle executing simple harmonic motion is shown in figure. The time period of simple harmonic motion is
View Solution
