In a rectangle ABCD (BC = 2 AB). The moment of inertia along which axes will be minimum
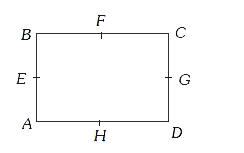
A
BC
B
BD
C
HF
D
EG
Video Solution
Text Solution
The correct Answer is:D
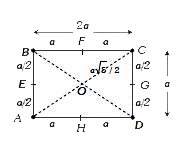
OC=√a2+(a2)2
=a√54=a2×√5
IEG→ is minimum, because distance is least.
|
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Angular Momentum)
52 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Work, Energy and Power)
44 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Angular Displacement, Velocity and Acceleration)
34 Videos
- NEWTON'S LAWS OF MOTIONBOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - ASSERTION & REASON
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assertion & Reason
15 Videos
Similar Questions
Knowledge Check
In a rectangle ABCD (BC=2AB). The moment of inertia along which the axis will be minimum
 ABCBBDCHFDEG
ABCBBDCHFDEGIn a rectangle ABCD (BC=2AB). The moment of inertia along which axis will be minimum
 AEGBHFCBDDBC
AEGBHFCBDDBCIn a rectangle ABCD (BC=2AB). The moment of inertia along which the axis will be minimum
 ABCBBDCHFDEG
ABCBBDCHFDEG
In a rectangle ABCD, AB=20cm , ∠BAC=60o . Calculate side BC .
View SolutionIn a rectangle ABCD(BC=2AB). The moment of inertia is minimum along axis through

View SolutionIn a rectangle ABCD(BC=2AB). The moment of inertia is maximum along axis through

View SolutionA wire of length l and mass m is bent in the form of a rectangle ABCD with ABBC=2. The moment of inertia of this wife frame about the side BC is
View SolutionA uniform plane sheet of metal in the form of a triangle ABC has BC>AB>AC. Its moment of inertia will be smallest
View Solution
