The moments of inertia of a non-uniform circular disc (of mass M and radius R) about four mutually perpendicular tangents AB, BC, CD, DA are I1,I2,I3 and I4, respectively (the square ABCD circumscribes the circle). The distance of the center of mass of the disc from its geometrical center is given by -
14MR√(I1−I3)2+(I2−I4)2
112MR√(I1−I3)2+(I2−I4)2
13MR√(I1−I2)2+(I2−I4)2
12MR√(I1+I3)2+(I2+I4)2
The correct Answer is:A
I1=ICM+M(R−y)2
I3=ICM+M(R+y)2
So, I3−I1=M[(R+y)2−(R−y)2] ...(i)
Same as
I4−I2=M[(R+x)2−(R−x)2] ...(ii)
By Distance of CM from centre of disc =x2+y2=14MR√(I1−I3)2+(I2−I4)2
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Angular Momentum)
52 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Work, Energy and Power)
44 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Angular Displacement, Velocity and Acceleration)
34 Videos
- NEWTON'S LAWS OF MOTIONBOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - ASSERTION & REASON
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assertion & Reason
15 Videos
Similar Questions
Knowledge Check
The moment of inertia of a uniform circular disc of mass M and of radius R about one of its diameter is
A14MR2B12MR2C23MR2D25MR2The moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
A12Mr2BMt2C25Mr2D14Mr2The moment of inertia of a disc of mass M and radius R about a tangent to its rim in its plane is
A23MR2B32MR2C45MR2D54MR2
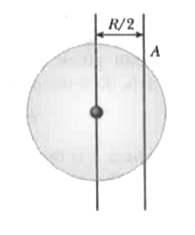
Find moment of inertia of a uniform ring (mass m, radius r) about chord AA' at distance R/2 from center.
View SolutionMoment of inertia of a thin semicircular disc (mass−M&radius=R) about an axis through point O and perpendicular to plane of disc, is given by :
 .
.
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionThe M.I. of a uniform semicircular disc of mass M and radius R about a line perpendicular to the plane of the disc and passing through the centre is
View SolutionThe moment of inertia of a uniform circular disc of radius R and mass M about an axis passing from the edge of the disc and normal to the disc is
View Solution
