A spring gun of spring constant 90 N/cm is compressed 12 cm by a ball of mass 16 g. If the trigger is pulled, the velocity of the ball is
50ms−1
9ms−1
40ms−1
90ms−1
The correct Answer is:D
To solve the problem step by step, we will follow the principles of energy conservation and the formulas related to springs and kinetic energy.
Step 1: Convert all units to SI units
- Spring constant (k): Given as 90 N/cm. Convert to N/m:
k=90N/cm=90×100N/m=9000N/m
- Compression (x): Given as 12 cm. Convert to meters:
x=12cm=12×10−2m=0.12m
- Mass (m): Given as 16 g. Convert to kg:
m=16g=16×10−3kg=0.016kg
Step 2: Calculate the potential energy stored in the spring
The potential energy (PE) stored in a compressed spring can be calculated using the formula:
PE=12kx2
Substituting the values:
PE=12×9000N/m×(0.12m)2
Calculating:
PE=12×9000×0.0144=64.8J
Step 3: Apply the conservation of energy principle
When the spring is released, all the potential energy converts into kinetic energy (KE) of the ball:
KE=12mv2
Setting the potential energy equal to the kinetic energy:
64.8=12×0.016×v2
Step 4: Solve for the velocity (v)
Rearranging the equation to solve for v2:
v2=64.8×20.016
Calculating:
v2=129.60.016=8100
Taking the square root to find v:
v=√8100=90m/s
Final Answer
The velocity of the ball when the trigger is pulled is:
90m/s
- Spring constant (k): Given as 90 N/cm. Convert to N/m:
k=90N/cm=90×100N/m=9000N/m
- Compression (x): Given as 12 cm. Convert to meters:
x=12cm=12×10−2m=0.12m
m=16g=16×10−3kg=0.016kg
The potential energy (PE) stored in a compressed spring can be calculated using the formula:
PE=12kx2
Substituting the values:
PE=12×9000N/m×(0.12m)2
Calculating:
PE=12×9000×0.0144=64.8J
When the spring is released, all the potential energy converts into kinetic energy (KE) of the ball:
KE=12mv2
Setting the potential energy equal to the kinetic energy:
64.8=12×0.016×v2
Rearranging the equation to solve for v2:
v2=64.8×20.016
Calculating:
v2=129.60.016=8100
Taking the square root to find v:
v=√8100=90m/s
The velocity of the ball when the trigger is pulled is:
90m/s
Topper's Solved these Questions
- WORK, ENERGY POWER AND COLLISIONBOOK - ERRORLESSCHAPTER - WORK, ENERGY POWER AND COLLISIONEXERCISE - NCERT BASED QUESTIONS (Power)
18 Videos
- WORK, ENERGY POWER AND COLLISIONBOOK - ERRORLESSCHAPTER - WORK, ENERGY POWER AND COLLISIONEXERCISE - NCERT BASED QUESTIONS (Elastic and Inelastic Collision)
44 Videos
- WORK, ENERGY POWER AND COLLISIONBOOK - ERRORLESSCHAPTER - WORK, ENERGY POWER AND COLLISIONEXERCISE - NCERT BASED QUESTIONS (Work Done by Variable Force)
26 Videos
- WAVES AND SOUND BOOK - ERRORLESSCHAPTER - WAVES AND SOUND EXERCISE - ASSERTION & REASON
25 Videos
Similar Questions
A spring gun has a spring constant of 80Ncm−1. The spring is compressed 12cm by a ball of mass 15g. How much is the potential energy of the spring ? If the trigger is pulled, what will be the velocity of ball ?
View SolutionA spring of spring constasnt 50 N/m is compressed from its natural position through 1 cm. Find the work done by the work done by the spring force on the agency compressing the spring.
View Solution
Knowledge Check
A spring gun of spring constant 90Ncm−1 is compressed 12 cm by a ball of mass 16 g. If the trigger is pulled, the velocity of the ball is
A50ms−1B40ms−1C60ms−1D90ms−1A toy gun uses a spring of spring constant 1000 N/m . If spring is compressed by an amount 10 cm before fire then how high can be bullet be fired if mass of each bullet is 10 g .
A30 mB40 mC50 mD60 mA massless spring of length l and spring constant k is placed vertically on a table. A ball of mass m is just kept on top of the spring. The maximum velocity of the ball is
Ag√mkBg√2mkCg2√mkDg√m2k
A spring is compressed by 10 cm by a ball of mass 20 g . What will be the potential energy of a spring if the force constant of the spring is 20 N cm−1 .
View SolutionIn a spring gun having spring constant 100 N/m a small ball 'B' of mass 100 g is put in its barrel (as shown in figure) by compressing the spring through 0.05 m. There should be a box placed at a distance 'd' on the ground so that the ball falls in it. If the ball leaves the gun horizontally at a height of 2 m above the ground. The value of d is ____ m. (g=10 m/s2)
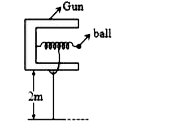
View SolutionIn a spring gun, a spring of force constant 200N/mis compressed 0.15 m. When fired, 80% of the elastic potential energy stored in the spring is eventually converted into kinetic energy of a 0.1 kg uniform ball that is rolling without slipping at the base of a ramp. The ball continues to roll without slipping up the ramp with 90% of the kinetic energy at the bottom converted into an increase in gravitational potential energy at the instant it stops.
(a) What is the speed of the ball's centre ofmass at the base of the ramp
(b) At this position, what is the speed of a point at the top of the ball?
(c ) What maximum vertical height up the ramp does the ball move?
View SolutionThere are two identical springs, each of spring constant 240 N/m, one of them is compressed by 10cm and the other is stretched by 10 cm. What is the difference in the potential energies stored in the two springs ?
View SolutionA 15gm ball is shot from a spring whose spring has a force constant of 600N/m. The spring is compressed by 5cm. The greater possible horizontal range of the ball for this compression is
View Solution
