A girl in a swing is 2.5m above ground at the maximum height and at 1.5m above the ground at the lowest point. Her maximum velocity in the swing is (g=10ms−2)
5√2ms−1
2√5ms−1
2√3ms−1
3√2ms−1
The correct Answer is:B
To solve the problem of finding the maximum velocity of a girl on a swing, we can use the principle of conservation of mechanical energy. Here’s a step-by-step solution:
Step 1: Identify the heights
- The maximum height of the swing above the ground is given as h=2.5m.
- The lowest point of the swing above the ground is given as h′=1.5m.
Step 2: Determine the change in height
- The change in height (Δh) when the swing moves from the lowest point to the maximum height can be calculated as:
Δh=h−h′=2.5m−1.5m=1.0m
Step 3: Apply the conservation of energy
- At the lowest point, all the energy is kinetic, and at the maximum height, all the energy is potential. Therefore, we can set up the equation:
K.E. at lowest point=P.E. at maximum height
- The kinetic energy (K.E.) at the lowest point is given by:
K.E.=12mv2max
- The potential energy (P.E.) at the maximum height is given by:
P.E.=mgh
- Thus, we can write:
12mv2max=mgΔh
Step 4: Simplify the equation
- We can cancel the mass m from both sides (assuming m≠0):
12v2max=gΔh
- Rearranging gives:
v2max=2gΔh
Step 5: Substitute the known values
- We know g=10m/s2 and Δh=1.0m:
v2max=2×10m/s2×1.0m=20m2/s2
Step 6: Calculate vmax
- Taking the square root of both sides gives:
vmax=√20=2√5m/s
Final Answer
- The maximum velocity of the girl in the swing at the lowest point is:
vmax=2√5m/s
---
- The maximum height of the swing above the ground is given as h=2.5m.
- The lowest point of the swing above the ground is given as h′=1.5m.
- The change in height (Δh) when the swing moves from the lowest point to the maximum height can be calculated as:
Δh=h−h′=2.5m−1.5m=1.0m
- At the lowest point, all the energy is kinetic, and at the maximum height, all the energy is potential. Therefore, we can set up the equation:
K.E. at lowest point=P.E. at maximum height
- The kinetic energy (K.E.) at the lowest point is given by:
K.E.=12mv2max
- The potential energy (P.E.) at the maximum height is given by:
P.E.=mgh
- Thus, we can write:
12mv2max=mgΔh
- We can cancel the mass m from both sides (assuming m≠0):
12v2max=gΔh
- Rearranging gives:
v2max=2gΔh
- We know g=10m/s2 and Δh=1.0m:
v2max=2×10m/s2×1.0m=20m2/s2
- Taking the square root of both sides gives:
vmax=√20=2√5m/s
- The maximum velocity of the girl in the swing at the lowest point is:
vmax=2√5m/s
Topper's Solved these Questions
- WORK, ENERGY POWER AND COLLISIONBOOK - ERRORLESSCHAPTER - WORK, ENERGY POWER AND COLLISIONEXERCISE - NCERT BASED QUESTIONS (Power)
18 Videos
- WORK, ENERGY POWER AND COLLISIONBOOK - ERRORLESSCHAPTER - WORK, ENERGY POWER AND COLLISIONEXERCISE - NCERT BASED QUESTIONS (Elastic and Inelastic Collision)
44 Videos
- WORK, ENERGY POWER AND COLLISIONBOOK - ERRORLESSCHAPTER - WORK, ENERGY POWER AND COLLISIONEXERCISE - NCERT BASED QUESTIONS (Work Done by Variable Force)
26 Videos
- WAVES AND SOUND BOOK - ERRORLESSCHAPTER - WAVES AND SOUND EXERCISE - ASSERTION & REASON
25 Videos
Similar Questions
A player kicks a football with an initial speed of25ms−1 at an angle of 45∘ from the ground. What are the maximum height and the time taken by the football to reach at the highest point during motion ? (Take g=10ms−2)
View SolutionA stone is projected from a point on the ground in such a way so as to hit a bird at height 3h and could attain a maximum height 4h above the ground. If at the instant of projection, the bird flies away horizontally with speed 10ms−1 and the stone still hits the bird while descending, then the horizontal velocity of stone is
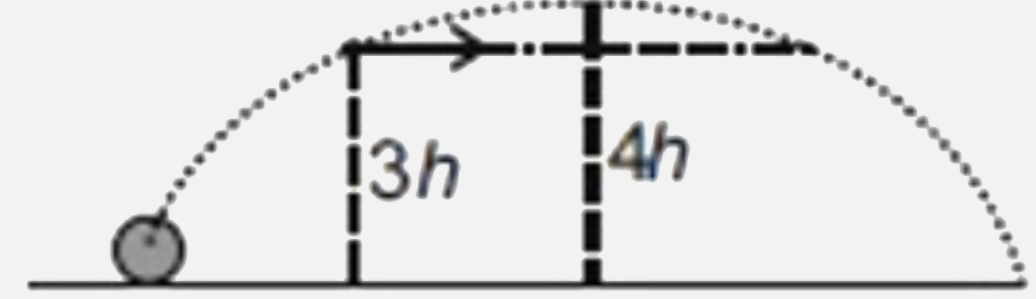
View Solution
Knowledge Check
A girl in a swing is 2.5 m above ground at the maximum height and at 1.5 m above the ground at the lowest point. Her maximum velocity in the swing is (g=10ms−2)
A5√2ms−1B2√5ms−1C2√3ms−1D3√2ms−1A girl in a swing is 2.5 m above ground at the maximum height and at 1.5 m above the ground at the lowest point, Her maximum velocity in the swing is (g=10ms−2)
A5√2ms−1B2√5ms−1C2√3ms−1D32ms−1A body swinging on a swing is 1 metre above the ground at the lowest point. He is 2m above the ground at the highest postiion. What is the velocity at the lowest point of the swing?
A√20ms−1B20ms−1C2ms−1D1ms−1
A porter lifts a luggage of 12 kg from the ground and puts it on his head 1.5 m above the ground. Calculate the work done by him on the luggage. (g=10ms−2)
View SolutionA child is swinging a swing. Minimum and maximum heights fo swing from the earth's surface are 0.75 m and 2 m respectively. The maximum velocity of this swing is
View SolutionA body is thrown vertically upward from a point A 125 m above the ground. It goes up to a maximum height of 250 m above the ground and passes through A on its downward journey. The velocity of the body when it is at a height of 70 m above the ground is (g=10m/s2)
View SolutionA porter lifts luggage of 20 kg from the ground and puts it on his head 2 m above the ground. Calculate the work done by him on the luggage. (take g =10 ms−2 )
View SolutionA cradle is 'h' meters above the ground at the lowest position and 'H' meters when it is at the highest point. If 'v' is the maximum speed of the swing of total mass 'm' the relation between 'h' and 'H' is
View Solution
