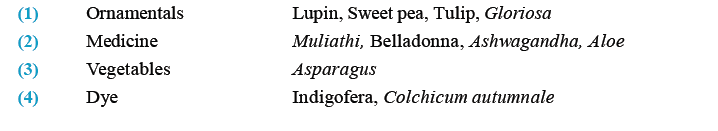Select the INCORRECT match.
cos2θ+11+cot2θ=1
(1+tan2θ)(1+sinθ)(1−sinθ)=1
tanθ+sinθtanθ−sinθ=secθ−1secθ+1
sin3θ+cos3θsinθ+cosθ+sinθcosθ=1
The correct Answer is:C
To solve the question of selecting the INCORRECT match from the given options, we will analyze each option step by step.
Step 1: Analyze Option 1
- The expression is cos2θ+11+cot2θ.
- We know that cot2θ=cos2θsin2θ.
- Therefore, 1+cot2θ=1+cos2θsin2θ=sin2θ+cos2θsin2θ=1sin2θ (using sin2θ+cos2θ=1).
- Thus, 11+cot2θ=sin2θ.
- Now, substituting back, we have cos2θ+sin2θ=1.
- Conclusion: Option 1 is correct.
Step 2: Analyze Option 2
- The expression is 1+tan2θ.
- We know that tan2θ=sin2θcos2θ.
- Therefore, 1+tan2θ=1+sin2θcos2θ=cos2θ+sin2θcos2θ=1cos2θ=sec2θ.
- Conclusion: Option 2 is correct.
Step 3: Analyze Option 3
- The expression is tanθ+sinθ.
- We know that tanθ=sinθcosθ.
- Therefore, tanθ+sinθ=sinθcosθ+sinθ=sinθ+sinθcosθcosθ=sinθ(1+cosθ)cosθ.
- This does not simplify to a standard identity.
- Conclusion: Option 3 is incorrect.
Step 4: Analyze Option 4
- The expression is sin3θ+cos3θsinθ+cosθ.
- We can apply the identity for the sum of cubes: a3+b3=(a+b)(a2−ab+b2).
- Here, a=sinθ and b=cosθ.
- Thus, sin3θ+cos3θ=(sinθ+cosθ)(sin2θ−sinθcosθ+cos2θ).
- The denominator sinθ+cosθ cancels out, leaving sin2θ−sinθcosθ+cos2θ=1−sinθcosθ.
- Conclusion: Option 4 is correct.
Final Conclusion:
- The incorrect match is Option 3.
- The expression is cos2θ+11+cot2θ.
- We know that cot2θ=cos2θsin2θ.
- Therefore, 1+cot2θ=1+cos2θsin2θ=sin2θ+cos2θsin2θ=1sin2θ (using sin2θ+cos2θ=1).
- Thus, 11+cot2θ=sin2θ.
- Now, substituting back, we have cos2θ+sin2θ=1.
- Conclusion: Option 1 is correct.
- The expression is 1+tan2θ.
- We know that tan2θ=sin2θcos2θ.
- Therefore, 1+tan2θ=1+sin2θcos2θ=cos2θ+sin2θcos2θ=1cos2θ=sec2θ.
- Conclusion: Option 2 is correct.
- The expression is tanθ+sinθ.
- We know that tanθ=sinθcosθ.
- Therefore, tanθ+sinθ=sinθcosθ+sinθ=sinθ+sinθcosθcosθ=sinθ(1+cosθ)cosθ.
- This does not simplify to a standard identity.
- Conclusion: Option 3 is incorrect.
- The expression is sin3θ+cos3θsinθ+cosθ.
- We can apply the identity for the sum of cubes: a3+b3=(a+b)(a2−ab+b2).
- Here, a=sinθ and b=cosθ.
- Thus, sin3θ+cos3θ=(sinθ+cosθ)(sin2θ−sinθcosθ+cos2θ).
- The denominator sinθ+cosθ cancels out, leaving sin2θ−sinθcosθ+cos2θ=1−sinθcosθ.
- Conclusion: Option 4 is correct.
- The incorrect match is Option 3.
Topper's Solved these Questions
- IMO QUESTION PAPER 2016 SET BBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2016 SET BEXERCISE - EVERYDAY MATHEMATICS
10 Videos
- IMO QUESTION PAPER 2016 SET BBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2016 SET BEXERCISE - ACHIEVERS SECTION
5 Videos
- IMO QUESTION PAPER 2016 SET ABOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2016 SET AEXERCISE - ACHIEVERS SECTION
5 Videos
- IMO QUESTION PAPER 2017 SET ABOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2017 SET AEXERCISE - Achievers Section
5 Videos
Similar Questions
Knowledge Check
Select an incorrect match.
APhycomycetes-Mucor, AlbugoBAscomycetes-Penicillium, AspergillusCBasidiomycetes-Puccinia,AgaricusDDeuteromycetes-Ustilago, ColletotrichumSelect an incorrect match.
APhycomycetes-Mucor, AlbugoBAscomycetes-Penicillium, AspergillusCBasidiomycetes-Puccinia,AgaricusDDeuteromycetes-Ustilago, ColletotrichumSelect an incorrect match:
APhycomycetes-Mucor, AlbugoBAscomycetes-Penicillium, AspergillusCBasidiomycetes-Puccinia,AgaricusDDeuteromycetes-Ustilago, Colletotrichum