Question

State 'T' for true and 'F' for false .
I. A sequence is an A.P ., if and only if the sum of its n terms is of the form $A{n}^2+Bn$ , where A and B are constants .
II. If 18, a, b , $-3$ are in A.P., then $a+b=15$ .
III If a,c,b are in A.P., then $2c=a+b$ .
IV .The $n^{th}$ term from the end of an A.P. is the ${(m-n+1)}^{th}$ term from the beginning , where m terms are in A.P.

Options

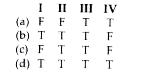
A. `{:("I","II","III","IV"),("F","F","T","T"):}`
B. `{:("I","II","III","IV"),("T","T","T","F"):}`
C. `{:("I","II","III","IV"),("F","T","T","F"):}`
D. `{:("I","II","III","IV"),("T","T","T","T"):}`

Answer

d