If AD is a median of a ΔABC and P is a point on AC such that ar (ΔADP) : ar (ΔABD) = 2 : 3, then ar (ΔPDC) : ar (ΔABC) is
1:6
1:5
2:5
3:5
The correct Answer is:A
To solve the problem step by step, we will follow the reasoning laid out in the video transcript.
Step 1: Understand the given information
We are given that AD is a median of triangle ABC, which means it divides triangle ABC into two equal areas, specifically triangles ABD and ADC.
Step 2: Assign area values
Let the area of triangle ABD be x. Since AD is a median, the area of triangle ADC will also be x. Therefore, the total area of triangle ABC is:
Area of △ABC=Area of △ABD+Area of △ADC=x+x=2x
Step 3: Use the given ratio of areas
We are given that the ratio of the area of triangle ADP to the area of triangle ABD is 2:3. This can be expressed mathematically as:
Area of △ADPArea of △ABD=23
Substituting the area of triangle ABD:
Area of △ADPx=23
From this, we can find the area of triangle ADP:
Area of △ADP=23x
Step 4: Find the area of triangle PDC
Now, we need to find the area of triangle PDC. We know that:
Area of △PDC=Area of △ADC−Area of △ADP
Substituting the known areas:
Area of △PDC=x−23x
Calculating this gives:
Area of △PDC=33x−23x=13x
Step 5: Find the ratio of areas
Now we need to find the ratio of the area of triangle PDC to the area of triangle ABC:
Area of △PDCArea of △ABC=13x2x
Simplifying this ratio:
=13⋅12=16
Step 6: Express the ratio in the required form
Thus, the ratio of the area of triangle PDC to the area of triangle ABC is:
Area of △PDC:Area of △ABC=1:6
Final Answer
The final answer is:
ar △PDC:ar △ABC=1:6
We are given that AD is a median of triangle ABC, which means it divides triangle ABC into two equal areas, specifically triangles ABD and ADC.
Let the area of triangle ABD be x. Since AD is a median, the area of triangle ADC will also be x. Therefore, the total area of triangle ABC is:
Area of △ABC=Area of △ABD+Area of △ADC=x+x=2x
We are given that the ratio of the area of triangle ADP to the area of triangle ABD is 2:3. This can be expressed mathematically as:
Area of △ADPArea of △ABD=23
Substituting the area of triangle ABD:
Area of △ADPx=23
From this, we can find the area of triangle ADP:
Area of △ADP=23x
Now, we need to find the area of triangle PDC. We know that:
Area of △PDC=Area of △ADC−Area of △ADP
Substituting the known areas:
Area of △PDC=x−23x
Calculating this gives:
Area of △PDC=33x−23x=13x
Now we need to find the ratio of the area of triangle PDC to the area of triangle ABC:
Area of △PDCArea of △ABC=13x2x
Simplifying this ratio:
=13⋅12=16
Thus, the ratio of the area of triangle PDC to the area of triangle ABC is:
Area of △PDC:Area of △ABC=1:6
The final answer is:
ar △PDC:ar △ABC=1:6
Topper's Solved these Questions
- IMO QUESTION PAPER 2020 SET 2BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2020 SET 2EXERCISE - Everyday Mathematics
10 Videos
- IMO QUESTION PAPER 2020 SET 2BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2020 SET 2EXERCISE - Achievers Section
5 Videos
- IMO QUESTION PAPER 2020 SET 1BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2020 SET 1EXERCISE - Achievers Section
5 Videos
- IMO QUESTION PAPER SET A 2017BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER SET A 2017EXERCISE - ARCHIEVERS SECTION
5 Videos
Similar Questions
AD is one of the medians of a ABC..X is any point on AD . Show that ar(ABX)=ar(ACX)
View SolutionIn △ABC ,AD is a median and P is a point on AD such that AP : PD = 3 : 4. Then ar(△BPD):ar(△ABC) is equal to:
त्रिभुज ABC में, AD एक माध्यिका है और P, AB पर स्थित ऐसा बिंदु है कि AP : PD = 3 : 4 है| ar(△BPD):ar(△ABC) ज्ञात करें |
View Solution
Knowledge Check
In the given figure, AD is the median and E is any point on AC, such that ar(ΔMDE) : ar(ΔABD) = 2 : 3, then find the ratio of ar(ΔEDC): ar(ΔABC).
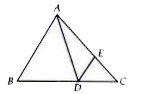 A3 : 4B1 : 6C6 : 1D4 : 3
A3 : 4B1 : 6C6 : 1D4 : 3In the given figure ar (ΔABC)= ar (ΔADE). AC is the median of ΔADE. If ar (ACE) =14cm2 then ar (ΔABC) = ?
 A14cm2B7cm2C21cm2D28cm2
A14cm2B7cm2C21cm2D28cm2It is given that ΔABC~ΔPRQandBCQR=23 then ar(ΔPQR)ar(ΔABC)=?
A23B32C49D94
ABC,DEAB=2:3 and ar(ΔDEF)=44sq.units then ar(ΔABC)is
View SolutionIn an equilateral ΔABC,D is the midpoint of AB and E is the midpoint of AC. Then, ar(ΔABC):ar(ΔADE)=?

View SolutionIn △ABC, AD is median and P is the point on AD such that AP : PD = 3 : 4, then ar(△APB):ar(△ABC) is equal to :
त्रिभुज ABC में, AD मध्यिका है तथा P, AD पर स्थित ऐसा बिंदु है कि AP : PD = 3 : 4 है, तो ar(△APB):ar(△ABC) का मान किसके बराबर होगा ?
View SolutionIn △ABC, AD is the median and G is a point on AD such that AG : GD = 2 : 1, then ar(△BDG):(△ABC) is equal to :
त्रिभुज ABC में, AD माध्यिका है तथा G, AD पर ऐसा बिंदु है कि AG : GD = 2 : 1 है, तो ar(△BDG):(△ABC) का मान ज्ञात करें |
View SolutionIn Δ ABC, D is the mid-point of AB and P is any point on BC. If CQ∣∣PD meets AB and Q (shown in figure), then prove that
ar(ΔBPQ)=12ar(ΔABC).

View Solution
