If C be the mid-point of a line segment AB, then AC= BC= (___) AB
3
12
2
14
The correct Answer is:B
To solve the problem, we need to determine the relationship between the lengths of segments AC, BC, and AB when C is the midpoint of line segment AB.
1. Identify the Midpoint:
Let A and B be two points on a line segment. C is defined as the midpoint of line segment AB.
2. Understanding the Midpoint:
By definition, if C is the midpoint of AB, it means that C divides the segment AB into two equal parts. Therefore, the lengths of segments AC and BC are equal.
AC=BC
3. Expressing AB in terms of AC and BC:
Since C is the midpoint, we can express the total length of segment AB as the sum of the lengths of segments AC and BC:
AB=AC+BC
4. Substituting Equal Lengths:
Since we established that AC = BC, we can substitute BC with AC in the equation:
AB=AC+AC=2⋅AC
5. Finding AC in terms of AB:
To find the length of AC in terms of AB, we can rearrange the equation:
AC=AB2
6. Conclusion:
Since AC = BC, we can conclude that:
AC=BC=12AB
Therefore, the blank in the question can be filled with 12.
Final Answer:
AC = BC = 12AB
Let A and B be two points on a line segment. C is defined as the midpoint of line segment AB.
By definition, if C is the midpoint of AB, it means that C divides the segment AB into two equal parts. Therefore, the lengths of segments AC and BC are equal.
AC=BC
Since C is the midpoint, we can express the total length of segment AB as the sum of the lengths of segments AC and BC:
AB=AC+BC
Since we established that AC = BC, we can substitute BC with AC in the equation:
AB=AC+AC=2⋅AC
To find the length of AC in terms of AB, we can rearrange the equation:
AC=AB2
Since AC = BC, we can conclude that:
AC=BC=12AB
Therefore, the blank in the question can be filled with 12.
AC = BC = 12AB
Topper's Solved these Questions
- INTRODUCTION TO EUCLID'S GEOMETRYBook:SCIENCE OLYMPIAD FOUNDATION Chapter:INTRODUCTION TO EUCLID'S GEOMETRYExercise:Achievers Section (HOTS)
Explore 3 Videos
- IMO QUESTION PAPER SET B 2019Book:SCIENCE OLYMPIAD FOUNDATION Chapter:IMO QUESTION PAPER SET B 2019Exercise:ACHIEVERS SECTION
Explore 5 Videos
- LINEAR EQUATIONS IN TWO VARIABLES Book:SCIENCE OLYMPIAD FOUNDATION Chapter:LINEAR EQUATIONS IN TWO VARIABLES Exercise:ACHIEVERS SECTION (HOTS)
Explore 2 Videos
Similar Questions
Knowledge Check
In the figure P(3, 2) is the mid-point of the line segment AB. What are the co-ordinates of A and B respectively:
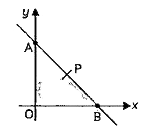 A(4,0) and (6, 0)B(0,4) and (6,0)C(0,4) and (0,6)D(0,-4) and (-6, 0)
A(4,0) and (6, 0)B(0,4) and (6,0)C(0,4) and (0,6)D(0,-4) and (-6, 0)
In give figur l||m and M is the mid-point of a line segment AB .Show that M is also the mid- point of any line segment CD,having its end points on l and m,respectively.
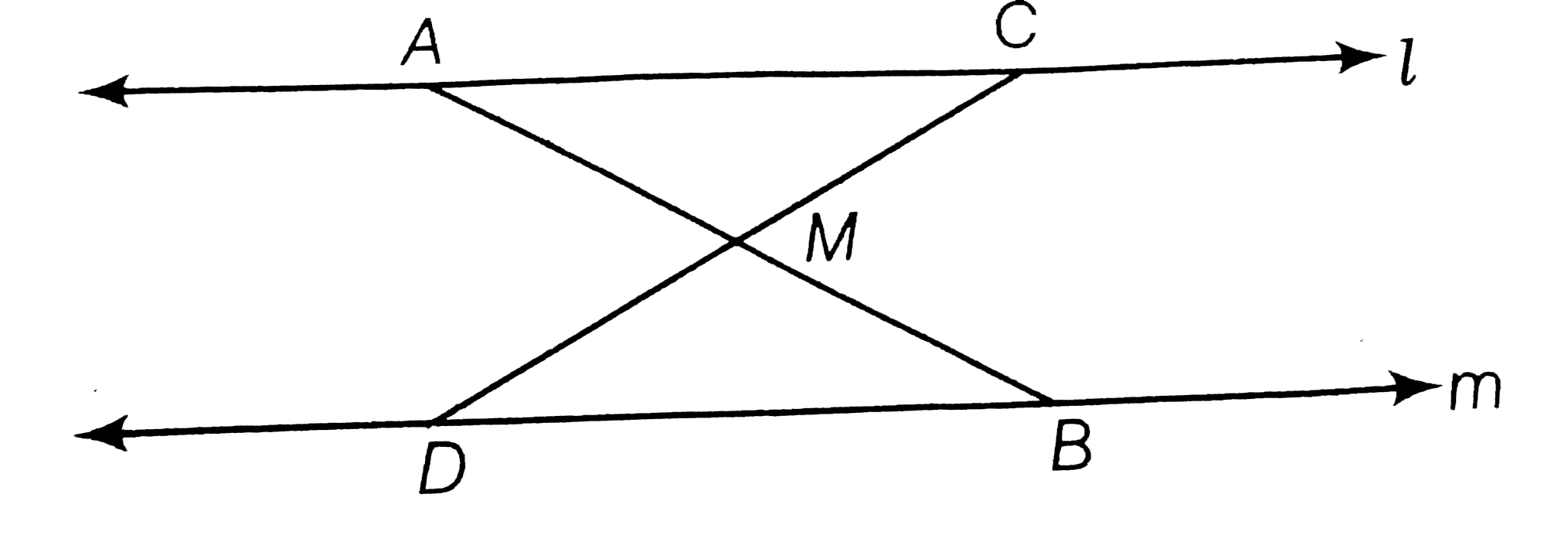
View SolutionIn figure l||m and M is the mid-point of the line segment AB. Prove that M is also the mid-point of line segment CD.

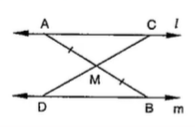
View SolutionIn Figure, lm and M is the mid-point of the line segment AB. Prove that M is also the mid-point of any line segment CD having its end-points on l and m respectively.
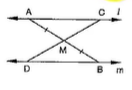
View SolutionIn Figure, l∣∣m and M is the mid-point of the line segment AB . Prove that M is also the mid-pooint of any line segment CD having its end-points on l and m respectively.
View SolutionThe position vectors of the points A,B with respect to O are ¯a and ¯b and c is mid point of line segment ¯¯¯¯¯¯AB then ¯¯¯¯¯¯OC=
View SolutionWhat is mid - point of line segment AB, where A (-5,0) and B(0,5) ?
View SolutionIn Question 4,
(If a point C lies between two points A and B such that AC = BC, then prove thatAC=12AB.Explain by drawing the figure).
Point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
View Solution