In Question 4,
(If a point C lies between two points A and B such that AC = BC, then prove thatAC=12AB.Explain by drawing the figure).
Point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
To prove that if a point C lies between two points A and B such that AC = BC, then AC = 1/2 AB, and to show that every line segment has one and only one midpoint, we can follow these steps:
1. Understanding the Given Information:
- We have three points: A, B, and C.
- Point C lies between points A and B.
- It is given that AC = BC.
2. Defining the Lengths:
- Let the length of AC be denoted as x.
- Since AC = BC, the length of BC is also x.
3. Finding the Length of AB:
- The total length of the line segment AB can be expressed as:
AB=AC+BC
- Substituting the values we have:
AB=x+x=2x
4. Expressing AC in Terms of AB:
- We can now express AC in terms of AB:
AC=12AB
- This shows that if AC = BC, then AC is indeed half of AB.
5. Defining Midpoint:
- By definition, a point C is called the midpoint of line segment AB if it satisfies the condition AC = BC.
6. Proving Uniqueness of the Midpoint:
- Assume there are two midpoints, C and D, on line segment AB.
- Since C is a midpoint, we have AC = BC and AC = 1/2 AB.
- Since D is also a midpoint, we have AD = BD and AD = 1/2 AB.
7. Using the Transitive Property:
- Since AC = 1/2 AB and AD = 1/2 AB, we can conclude:
AC=AD
- This implies that the lengths AC and AD are equal.
8. Using the Segment Addition Postulate:
- We can express AC as:
AC=AD+DC
- Since AC = AD, we can substitute:
AD=AD+DC
9. Subtracting Equal Quantities:
- By subtracting AD from both sides, we get:
0=DC
- This means that points C and D coincide, proving that there is only one midpoint.
10. Conclusion:
- Therefore, we conclude that every line segment has one and only one midpoint.
- We have three points: A, B, and C.
- Point C lies between points A and B.
- It is given that AC = BC.
- Let the length of AC be denoted as x.
- Since AC = BC, the length of BC is also x.
- The total length of the line segment AB can be expressed as:
AB=AC+BC
- Substituting the values we have:
AB=x+x=2x
- We can now express AC in terms of AB:
AC=12AB
- This shows that if AC = BC, then AC is indeed half of AB.
- By definition, a point C is called the midpoint of line segment AB if it satisfies the condition AC = BC.
- Assume there are two midpoints, C and D, on line segment AB.
- Since C is a midpoint, we have AC = BC and AC = 1/2 AB.
- Since D is also a midpoint, we have AD = BD and AD = 1/2 AB.
- Since AC = 1/2 AB and AD = 1/2 AB, we can conclude:
AC=AD
- This implies that the lengths AC and AD are equal.
- We can express AC as:
AC=AD+DC
- Since AC = AD, we can substitute:
AD=AD+DC
- By subtracting AD from both sides, we get:
0=DC
- This means that points C and D coincide, proving that there is only one midpoint.
- Therefore, we conclude that every line segment has one and only one midpoint.
Similar Questions
In question I, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.

View SolutionIn Question 4,
(If a point C lies between two points A and B such that AC = BC, then prove thatAC=12AB.Explain by drawing the figure).
Point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
View Solution
Knowledge Check
A point C is called the midpoint of a line segment ¯¯¯¯¯¯AB if
AC is an intrerior points of ABBAC =CBCC is an interior point of AB such that ¯¯¯¯¯¯AC=¯¯¯¯¯¯CBDAC+CB=ABIn the figure P(3, 2) is the mid-point of the line segment AB. What are the co-ordinates of A and B respectively:
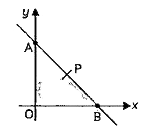 A(4,0) and (6, 0)B(0,4) and (6,0)C(0,4) and (0,6)D(0,-4) and (-6, 0)
A(4,0) and (6, 0)B(0,4) and (6,0)C(0,4) and (0,6)D(0,-4) and (-6, 0)
Mid point of a line Segment
View SolutionIf A, B and C are three points on a line and B is between A and C then prove that AC - BC = AB.
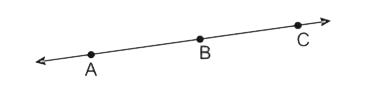
View SolutionIf A. B and C are three points on a line, and B lies between A and C then prove that AB−BC=AC.
View SolutionIn figure l||m and M is the mid-point of the line segment AB. Prove that M is also the mid-point of line segment CD.

View SolutionIf A, B and C are three poins on a line and B lies between A and C, then prove that AB + BC = AC.

View SolutionIn the given figure, P (4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.
View Solution
