
In the given figure, PQRS is a rhombus whose diagonal PR and QS are along coordinate axes and PR = 12 units and QS = 6 units.
Now, if T is a point which is 5 units right and 2 units above S, then find
(i) sum of abscissae of P and T.
(ii) sum of ordinates of Q, R and T.
(i)(ii)−12
(i)(ii)1−2
(i)(ii)12
(i)(ii)−1−2
The correct Answer is:A
Step by step video, text & image solution for In the given figure, PQRS is a rhombus whose diagonal PR and QS are along coordinate axes and PR = 12 units and QS = 6 units. Now, if T is a point which is 5 units right and 2 units above S, then find (i) sum of abscissae of P and T. (ii) sum of ordinates of Q, R and T. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COORDINATE GEOMETRY BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - COORDINATE GEOMETRY EXERCISE - ACHIEVERS SECTION (HOTS) (TRUE/FALSE)
1 Video
- CONSTRUCTIONSBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - CONSTRUCTIONSEXERCISE - Achievers Section (HOTS)
5 Videos
- HERON'S FORMULABOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - HERON'S FORMULAEXERCISE - Achievers Section (HOTS)
3 Videos
Similar Questions
In Figure, PQRS is a rhombus in which the diagonal PR is produced to T. If ∠SRT=1520, find x, y and z

View SolutionIn the given figure, PQRS is a straight line R is the mid-point of QS and Q is the mid-point of PS. S is (6,5), R is (3, 5) and T is (4,8). Find the length of median TU. QRS
View Solution
Knowledge Check
Area of rhombus is 96cm2 and one of its diagonals is 12 cm . Find the side of the rhombus .
The following steps are involved in solving the above problem . Arrange them in sequential order .
(A) Let PQRS be a rhombus ,PR = 12 cm , and the diagonals PR and QS intersect at T .
(B) Area of the rhombus = 12×PR×QR=96
(C ) ⇒QS=16cm
(D ) PTQ is a right triangle and PQ2=62+82⇒PQ=10cm .
(E ) PT = PR2=6cmandQT=QS2=8 cmAABCDEBABECDCABCEDDACEBD
In the given figure , PQR is an equilateral triangle with side as 12 cm . S and T are the mid points of the sides PQ and PR respectively . What ist he area (in cm2) of the shaded region ?
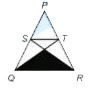
View SolutionThe area of a circle whose radius is the diagonal of a square whose area is 4 sq. units is 16π sq.units (b) 4π sq.units (c) 6π sq.units (d) 8π sq.units
View SolutionThe radius of base and curved surface area of a right cylinder is 'r' units and 4πrh square units respectively. The height of the cylinder is h2 units (b) h units (c) 2h units (d) 4h units
View SolutionDirections: Study the following information to answer the given Questions: Eight persons are sitting in a round table viz. P, Q, R, S, T, U, V, and W. All are facing inside the table. They all have different ages viz. 8, 10, 15, 11, 12, 13, 23 and 25 but not necessarily in the same order. T is sitting 2nd to the left of P whose age is an odd number. Q is sitting beside the one whose age is not a prime number. There are two persons between R and Q. The person whose age is multiple of 5 is sitting opposite to each other. V’s age is cubic number and sits immediate left of Q. S is not the immediate neighbour of T and Q. R is to the immediate left of T. The sum of ages of W and T is 23. V sits 3rd to the right of T whose age is a prime number. W’s age is the second youngest among all. U’s age is the square number and sits beside the person whose age is a prime number. The sum of the age of R and V is 19. The age of S is 12. The person whose age 10 years is not a neighbor of T. The age of Q is less than the age of P.
What is the sum of ages of P and R?
View SolutionIn figure LM is a line parallel to the Y-axis at a distance of 3 units .
(i) What are the coordinates of the points P,R and Q ?
(ii) What is the difference between the abscissa of the points L and M ?
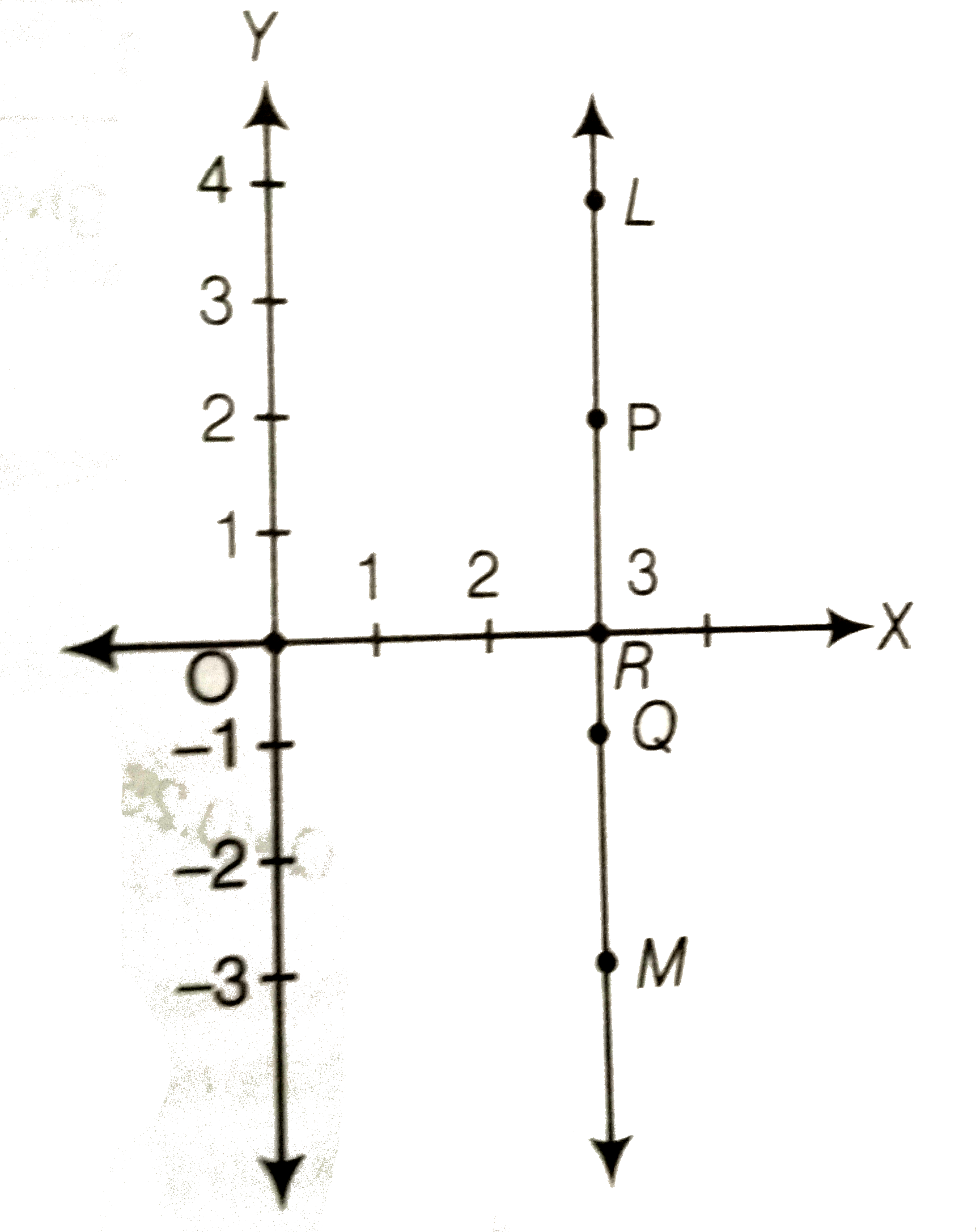
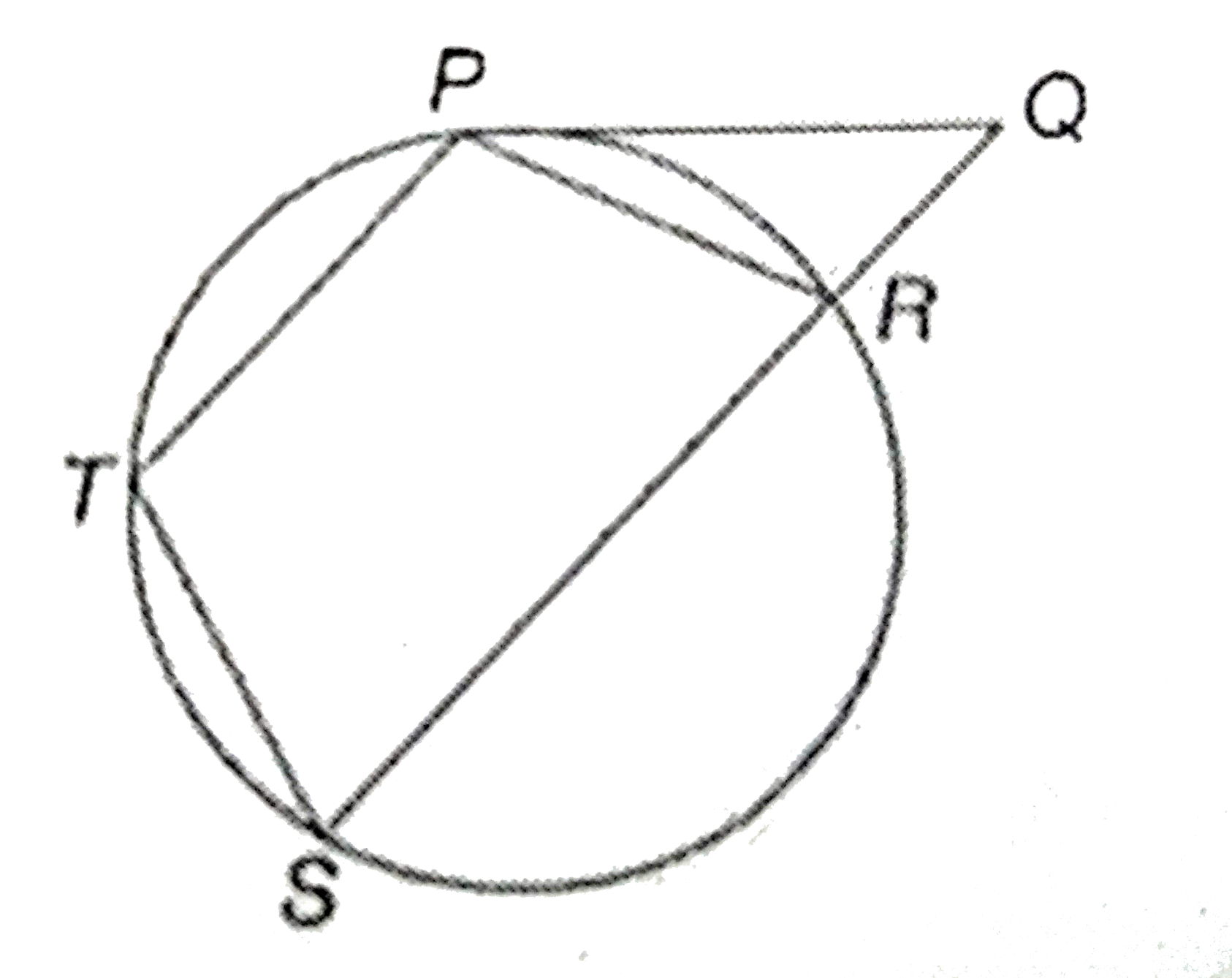
View SolutionIn the figure above (not to scale), PQ is a tangent segment to the circle at P.If P,R,S and T are concyclic points, ∠QPR=40∘ and PR=RQ then find ∠PTS.
View SolutionIn the given figure, a triangle PQR is drawn to circumscribe a circle of radius √3cm such that segments RS and QS into which QR is divided by the point of contact S are of lengths 5cm and 3cm respectively. If the area of ΔPQR is 10√3cm2, then find the sides PQ and PR.
View Solution
