Match the figures given in the Column 1 with their line(s) of symmetry given in Column 2
Column 1Column 2(P) Equilateral triangle(1) 0(Q) Square(2) 3(R) Parallelogram(3) 2(S) Rhombus(4) 4
(P)→(2),(Q)→(4),(R)→(1),(S)→(3)
(P)→(2),(Q)→(4),(R)→(3),(S)→(1)
(P)→(4),(Q)→(2),(R)→(1),(S)→(3)
(P)→(2),(Q)→(1),(R)→(4),(S)→(3)
The correct Answer is:A
To solve the problem of matching the figures in Column 1 with their corresponding lines of symmetry in Column 2, let's analyze each figure step by step.
Step 1: Analyze the Equilateral Triangle (P)
An equilateral triangle has three equal sides and three equal angles. The lines of symmetry for an equilateral triangle can be drawn from each vertex to the midpoint of the opposite side.
- Lines of Symmetry: 3
Step 2: Analyze the Square (Q)
A square has four equal sides and four right angles. The lines of symmetry in a square can be drawn in the following ways:
1. Vertical line through the center.
2. Horizontal line through the center.
3. Diagonal line from one corner to the opposite corner (two diagonals).
- Lines of Symmetry: 4
Step 3: Analyze the Parallelogram (R)
A parallelogram has opposite sides that are equal and parallel, but it does not have lines of symmetry like a square or triangle. The only line of symmetry in a general parallelogram is when it is a rectangle, but in a general case, it has no lines of symmetry.
- Lines of Symmetry: 0
Step 4: Analyze the Rhombus (S)
A rhombus has all sides equal, similar to a square, but the angles are not necessarily right angles. The lines of symmetry in a rhombus can be drawn along the diagonals.
- Lines of Symmetry: 2
Summary of Matches
Now, we can summarize the matches:
- (P) Equilateral triangle → (2) 3 lines of symmetry
- (Q) Square → (4) 4 lines of symmetry
- (R) Parallelogram → (1) 0 lines of symmetry
- (S) Rhombus → (3) 2 lines of symmetry
Final Matching
- P → 2
- Q → 4
- R → 1
- S → 3
An equilateral triangle has three equal sides and three equal angles. The lines of symmetry for an equilateral triangle can be drawn from each vertex to the midpoint of the opposite side.
A square has four equal sides and four right angles. The lines of symmetry in a square can be drawn in the following ways:
1. Vertical line through the center.
2. Horizontal line through the center.
3. Diagonal line from one corner to the opposite corner (two diagonals).
A parallelogram has opposite sides that are equal and parallel, but it does not have lines of symmetry like a square or triangle. The only line of symmetry in a general parallelogram is when it is a rectangle, but in a general case, it has no lines of symmetry.
A rhombus has all sides equal, similar to a square, but the angles are not necessarily right angles. The lines of symmetry in a rhombus can be drawn along the diagonals.
Now, we can summarize the matches:
- (P) Equilateral triangle → (2) 3 lines of symmetry
- (Q) Square → (4) 4 lines of symmetry
- (R) Parallelogram → (1) 0 lines of symmetry
- (S) Rhombus → (3) 2 lines of symmetry
- P → 2
- Q → 4
- R → 1
- S → 3
Topper's Solved these Questions
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2020-21 SET AEXERCISE - Everyday mathematics10videos
IMO QUESTION PAPER 2020-21 SET A
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2020EXERCISE - Achievers section (HOTS)5videos
IMO QUESTION PAPER 2020
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - INTEGERSEXERCISE - ACHIEVERS SECTION (HOTS)5videos
INTEGERS
Similar Questions
Match the ions given in column 1 with their nature given in Column II.
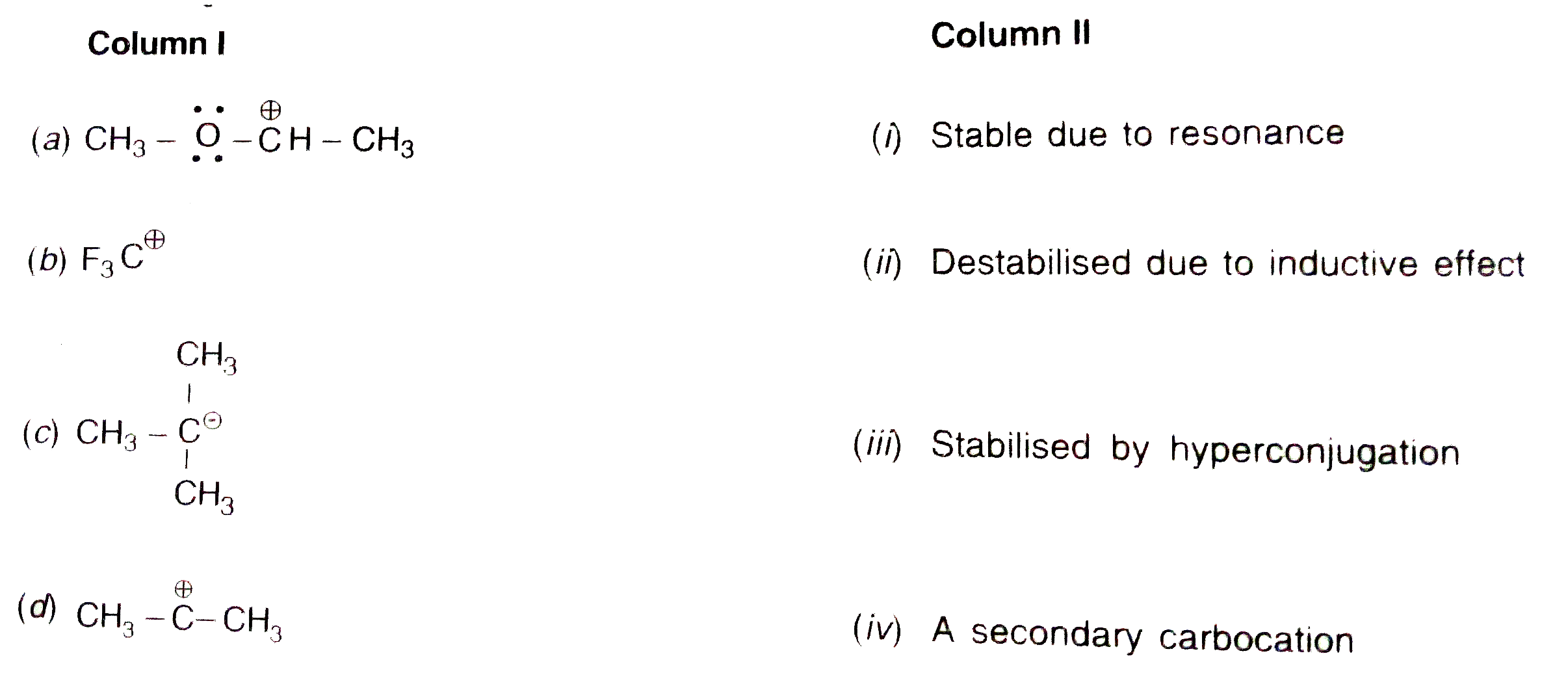 View Solution
View SolutionMatch the entries of Column 1 with those of Column 2.
 View Solution
View SolutionMatch the entries of Column 1 with those of Column 2.
 View Solution
View SolutionMatch the entries of Column 1 with those of Column 2.
 View Solution
View SolutionMatch the entries of Column 1 with those of Column 2.
 View Solution
View SolutionMatch the entries of Column 1 with those of Column 2.
 View Solution
View SolutionMatch the entries of Column 1 with those of Column 2.
 View Solution
View SolutionMatch the entries of Column 1 with those of Column 2.
 View Solution
View SolutionMatch the entries of Column 1 with those of Column 2.
 View Solution
View SolutionMatch the entries of Column 1 with those of Column 2.
 View Solution
View Solution
