In ΔABC, D is the midpoint of BC and G is the centroid. If GD=5 cm, then the length of AD is:
10 cm
12 cm
15 cm
20 cm
To solve the problem, we need to find the length of AD in triangle ABC where D is the midpoint of BC and G is the centroid. Given that GD = 5 cm, we can use the properties of centroids and medians to find AD.
1. Understanding the Properties of the Centroid:
- The centroid (G) of a triangle divides each median into two segments, one of which is twice the length of the other. Specifically, if AG is the segment from vertex A to the centroid G, and GD is the segment from G to the midpoint D of side BC, then the ratio AG:GD is 2:1.
2. Setting Up the Ratio:
- We can express the relationship as:
AGGD=21
- This means that AG is twice the length of GD.
3. Substituting the Known Value:
- We know that GD = 5 cm. Substituting this value into the ratio gives:
AG=2×GD=2×5 cm=10 cm
4. Finding the Length of AD:
- The length of AD can be found by adding the lengths of AG and GD:
AD=AG+GD=10 cm+5 cm=15 cm
5. Conclusion:
- Therefore, the length of AD is:
15 cm
- The centroid (G) of a triangle divides each median into two segments, one of which is twice the length of the other. Specifically, if AG is the segment from vertex A to the centroid G, and GD is the segment from G to the midpoint D of side BC, then the ratio AG:GD is 2:1.
- We can express the relationship as:
AGGD=21
- This means that AG is twice the length of GD.
- We know that GD = 5 cm. Substituting this value into the ratio gives:
AG=2×GD=2×5 cm=10 cm
- The length of AD can be found by adding the lengths of AG and GD:
AD=AG+GD=10 cm+5 cm=15 cm
- Therefore, the length of AD is:
15 cm
Similar Questions
In ΔABC, ∠B=90∘. D is the midpoint of hypotenuse AC. If BD=4.5cm, then find the length of hypotenuse AC.
View SolutionIn a ΔABC, D, E and F are the midpoints of BC, CA and AB respectively. If the lengths of side AB, BC and CA are 7 cm, 8 cm and 9 cm respectively, the perimeter of ΔDEF is a cm. The value of a/2 is
View Solution
Knowledge Check
In ΔABC,D is the mid-point of BC . Length AD is 27 cm . N is a point in AD such that the length of DN is 12 cm . The distance of N from the centroid of ΔABC is equal to
A3 cmB6 cmC9 cmD15 cmIn ΔABC,∠B is right angle and D is the mid-point of the side AC . If AB = 6 cm , BC = 8 cm , then the length of BD is
A4 cmB5 cmC8 cmD12 cmIn △ABC, if D is the midpoint of BC and E is the midpoint of AD then ar(△BED) = ?
 A12ar(△ABC)B13ar(△ABC)C14ar(△ABC)D23ar(△ABC)
A12ar(△ABC)B13ar(△ABC)C14ar(△ABC)D23ar(△ABC)
In ΔABC,D is the mid-point of BC . Length AD is 27 cm . N is a point in AD such that the length of DN is 12 cm . The distance of N from the centroid of ΔABC is equal to
View SolutionIn the given Fig. 3, in ΔABC,DandE are the mid point of the sides AB and AC respectively. Find the length of DE. Prove that DE=12BC.
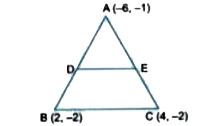
View SolutionIn ΔABC,AB=12cm,BC=16cm and CA=20cm If D is the mid point of AC then the length of BD is
View SolutionIn a ΔABC,D is the mid - point of BC and E is mid - point of AD, BF passes through E. What is the ratio of AF:FC?

View SolutionIn a ΔABC,D,EandF are respectively the mid-points of BC, CA and AB. If the lengths of side AB, BC and CA are 7 cm, 8 cm and 9 cm respectively, find the permeter of ΔDEF.
View Solution
