Magnetic Induced Emf is equal to ?
dϕ/dt
dm/dt
dϕ+dt
dl∗dt
The correct Answer is:A
To determine the magnetic induced EMF, we can follow these steps:
Step 1: Understand the Concept of Magnetic Flux
Magnetic flux (Φ) is defined as the product of the magnetic field (B) and the area (A) through which the field lines pass, taking into account the angle (θ) between the magnetic field and the normal to the surface:
Φ=B⋅A⋅cos(θ)
Step 2: Define Induced EMF
According to Faraday's law of electromagnetic induction, the induced electromotive force (EMF) in a closed loop is equal to the negative rate of change of magnetic flux through the loop:
Induced EMF=−dΦdt
Step 3: Apply the Concept
The induced EMF can be expressed as:
Induced EMF=−d(B⋅A⋅cos(θ))dt
However, for the purpose of this question, we are primarily concerned with the rate of change of magnetic flux itself, which simplifies to:
Induced EMF=dΦdt
Step 4: Identify the Correct Option
From the options provided, the correct expression for magnetic induced EMF is:
Induced EMF=dΦdt
This corresponds to the first option given in the question.
Conclusion
Thus, the magnetic induced EMF is equal to the rate of change of magnetic flux with respect to time:
Induced EMF=dΦdt
---
Magnetic flux (Φ) is defined as the product of the magnetic field (B) and the area (A) through which the field lines pass, taking into account the angle (θ) between the magnetic field and the normal to the surface:
Φ=B⋅A⋅cos(θ)
According to Faraday's law of electromagnetic induction, the induced electromotive force (EMF) in a closed loop is equal to the negative rate of change of magnetic flux through the loop:
Induced EMF=−dΦdt
The induced EMF can be expressed as:
Induced EMF=−d(B⋅A⋅cos(θ))dt
However, for the purpose of this question, we are primarily concerned with the rate of change of magnetic flux itself, which simplifies to:
Induced EMF=dΦdt
From the options provided, the correct expression for magnetic induced EMF is:
Induced EMF=dΦdt
This corresponds to the first option given in the question.
Thus, the magnetic induced EMF is equal to the rate of change of magnetic flux with respect to time:
Induced EMF=dΦdt
Similar Questions
The magnetic flux linked with a coil (in Wb) is given by the equation ϕ=5t2+3t+16 . The magnetic of induced emf in the coil at fourth second will be
View SolutionFind the emf induced in the coil shown in figure.The magnetic field is perpendicular to the plane of the coil and is constant.
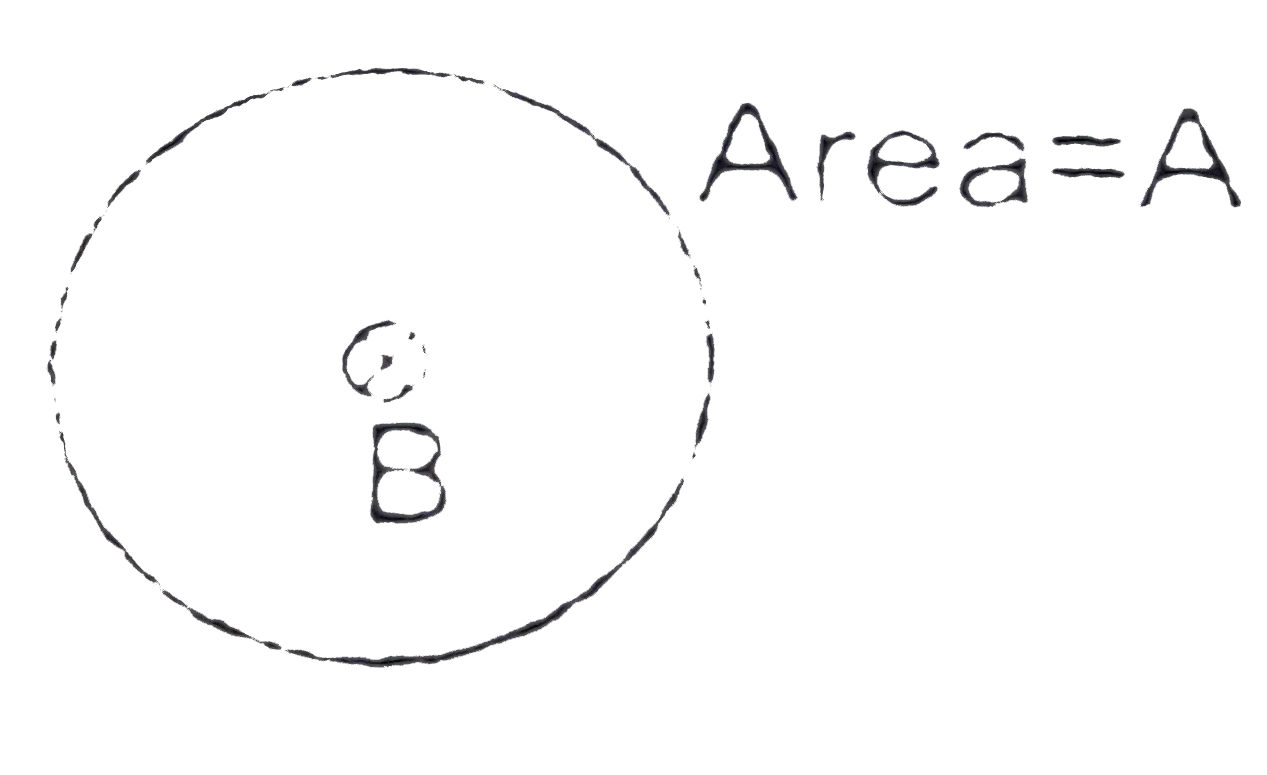
View Solution
Knowledge Check
When a rate of change of current in a circuit is unity, the induced emf is equal to
Athickness of coilBnumber of turns in coilCcoefficinet of self inductanceDtotal flux linked with coil
A: There may be an induced emf in a loop without induced current.
R: Induced current depends on the resistance of the loop as well.
View SolutionA magnetic flux of 500 microweber passing through a 200 turn coil is reversed in 20×10−3s. The average induced emf in the coil (in volt) is
View SolutionA rod of length l is translating at a velocity v making an angle θ with its length. A uniform magnetic field B exists in a direction perpendicular to the plane of motion. Calculate the emf induced In the rod, Draw a figure representing the induced emf by on equivalent battery.


View SolutionAt time t=0 magnetic Field of 1000 Gausses is passing perpendicularly through the area defined by the closed loop shown in the Figure. If the magnetic Field reduces linearly to 500 Gausses, in the next 5s, then induces EMF in the loop is:
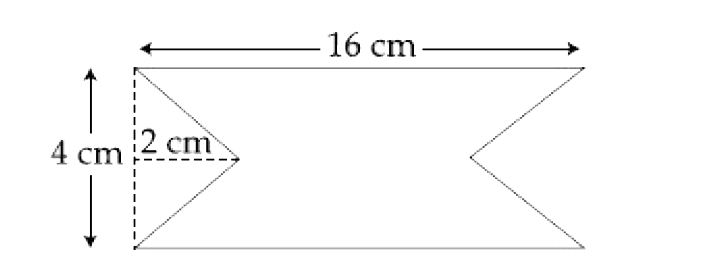
View SolutionA rod lies across frictionless rails in a uniform magnetic field →B as shown in figure. The rod moves to the right with speed V. In order to make the induced emf in the circuit to be zero, the magnitude of the magnetic field should

View SolutionAssertion If a loop is placed in a non-uniform (with respect to position) magnetic field, then induced emf is produced in the loop.
Reason In a non-uniform magnetic field, magnetic flux passing through the loop will change. Therefore, induced emf is produced.
View SolutionWhy the induced emf is also called as back emf?
View Solution
