Question

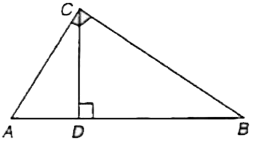
In $\Delta ABC,\angle C={90}^{\circ }$. D is a point on CA from which a perpendicular drawn to AB meets it at E. If $\angle EDA=\angle ABC$, BC = a cm., AD = x cm., AE = y cm., BE = Z cm. then DE = ……..cm.

Options

A. `(ay)/(z+x)`
B. `(az)/(x+y)`
C. `(ax)/(y+z)`
D. None of these

Explanation

To solve the problem, we will use the properties of similar triangles. Let's break down the solution step by step.

1. Draw Triangle ABC:
- Start by drawing triangle ABC with angle C = 90 degrees. Let A be at the top, B to the right, and C at the bottom left.

2. Identify Points:
- Mark point D on line segment CA. From point D, draw a perpendicular line to line segment AB, which meets AB at point E.

3. Label the Sides:
- According to the problem, we have:
- BC = a cm
- AD = x cm
- AE = y cm
- BE = z cm

4. Use the Angle-Angle (AA) Similarity Criterion:
- Since angle C = 90 degrees and angle EDA = angle ABC, we can say that triangle AED is similar to triangle ABC by the AA similarity criterion.

5. Set Up Proportions:
- From the similarity of triangles, we have:
\( \frac{DE}{BC} = \frac{AD}{AB} \)
- Here, we know:
- BC = a cm
- AD = x cm
- AB = AE + BE = y + z cm

6. Substitute Known Values:
- Substitute the known values into the proportion:
\( \frac{DE}{a} = \frac{x}{y + z} \)

7. Solve for DE:
- Cross-multiply to find DE:
\( DE = \frac{a \cdot x}{y + z} \)

Final Answer:
Thus, the length of DE is:
\( DE = \frac{a \cdot x}{y + z} \text{ cm} \)

---