Question

12 सेमी व्यास वाले काँच के ठोस गोले पर समान्तर किरणें आपतित हैं। अन्तिम रूप से ये किरणे अपवर्तन के पश्चात् कहाँ पर केन्द्रित होंगी?(काँच का अपवर्तनांक: 1.5)

Explanation

काँच का ठोस गोला एक उत्तल लेन्स है, परन्तु यह पतला नहीं है, अतः हम इस लेन्स के लिए सूत्र `(1)/(v)-(1)/(u)=(1)/(f)` का प्रयोग नहीं कर सकते हैं इसके लिए गोले के दोनों तलों पर होने वाले अपवर्तन पर अलग-अलग विचार करना होगा।
माना `P_(1)` तथा `P_(2)` गोले के विपरीत पृष्ठों के ध्रुव तथा C केन्द्र है।
गोले के प्रथम पृष्ठ पर वायु से काँच में अपवर्तन के लिए
`(n)/(v)-(1)/(u)=(n-1)/(R)`
यहाँ वस्तु की ध्रुव `P_(1)` से दूरी `u=oo` (किरणें समान्तर हैं)
`R=+P_(1)C=+6 ` सेमी, `n=1.5` (`because` व्यास = 12 सेमी)
अत: `(1.5)/(v)-(1)/(oo)=(1.5-1)/(6)`
अथवा `(1.5)/(v)=(0.5)/(6)`
अथवा `v=(1.5xx6)/(0.5)=+18` सेमी।
अतः समान्तर किरणें प्रथम पृष्ठ से अपवर्तन के पश्चात् इस पृष्ठ से पीछे की ओर ध्रुव `P_(1)` से 18 सेमी की दूरी पर बिन्दु I. पर केन्द्रित होंगी अर्थात् `P_(1)I.=18` सेमी होगा।
बिन्दु I. दूसरे पृष्ठ के लिए आभासी वस्तु का कार्य करेगा।

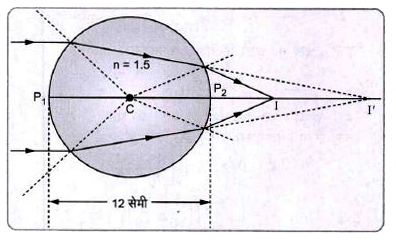
दूसरे पृष्ठ पर काँच से वायु में अपवर्तन के लिए `n.=(1)/(""_(a)n_(g))=(1)/(1.5)=(2)/(3)`
वस्तु I. की ध्रुव `P_(2)` से दूरी `u=+P_(2)I.=P_(1)I.-P_(1)P_(2)=18-12=+6` सेमी `(becauseP_(1)I.=18" सेमी")`
जबकि `R=-P_(2)C=-6` सेमी
अतः `(n.)/(v)-(1)/(u)=(n.-1)/(R)` से, `(2)/(3v)-(1)/(6)=(2/3-1)(-6)`
अथवा `(2)/(3v)=1/6+(1)/(18)=(2)/(9)`
अथवा `v=(9)/(3)=+3.0` सेमी
अतः द्वितीय पृष्ठ पर अपवर्तन के पश्चात् किरणे अन्तिम रूप से गोले के बाहर ध्रुव `P_(2)` से 3.0 सेमी की दूरी पर बिन्दु I पर केन्द्रित होंगी।