Study the following information carefully and answer the given questions.
Following data refers to total 2000 people who visited a mall on Saturday for the following activities: Movies, Dine- out and Shopping. A person may engage in one or more than one activity. 60% of the total number of people dined out and 54% of the total number of people went for Shopping (out of which 500 went for only Shopping).-The number of people who went for only Movies was half of that who went for both Movies and Dine-out -(but not shopping), and those who went for all activities are equal to those who went for both Shopping and Dine-out (but not Movies). 100 people went for both Shopping and Movies} (but not Dine-out).
What is the number of people who went for only Dine-
350
360
320
400
The correct Answer is:C
To solve the problem step by step, we will analyze the information provided and use it to find the number of people who went for only Dine-out.
Step 1: Calculate the total number of people who dined out and went shopping.
- Total number of people = 2000
- Percentage of people who dined out = 60%
- Number of people who dined out = 60% of 2000 = 0.6 * 2000 = 1200
- Percentage of people who went shopping = 54%
- Number of people who went shopping = 54% of 2000 = 0.54 * 2000 = 1080
Step 2: Determine the number of people who went for only shopping.
- It is given that 500 people went for only shopping.
Step 3: Set up variables for the other groups.
- Let:
- x = number of people who went for both Movies and Dine-out (but not shopping)
- y = number of people who went for all three activities
- z = number of people who went for both Shopping and Dine-out (but not Movies)
Step 4: Establish relationships based on the information given.
- The number of people who went for only Movies = x2 (half of those who went for both Movies and Dine-out).
- We know that y=z (the number of people who went for all activities is equal to those who went for both Shopping and Dine-out).
- It is also given that 100 people went for both Shopping and Movies (but not Dine-out).
Step 5: Set up equations based on the total number of people who went shopping.
- Total people who went shopping = 500 (only shopping) + 100 (shopping and movies) + z (shopping and dine-out) + y (all three activities).
- Therefore, we have:
500+100+z+y=1080
Since y=z, we can substitute y with z:
500+100+z+z=1080⟹600+2z=1080⟹2z=480⟹z=240
Thus, y=240.
Step 6: Find the value of x.
- Now we can find x using the total number of people who dined out:
- Total people who dined out = 1200
- This includes:
- 500 (only dine-out)
- x (dine-out and movies)
- z=240 (dine-out and shopping)
- y=240 (all three activities)
Therefore:
500+x+240+240=1200⟹500+x+480=1200⟹x=1200−980=220
Step 7: Calculate the number of people who went for only Dine-out.
- Now we can find the number of people who went for only Dine-out:
Only Dine-out=Total Dine-out−(Only Shopping+Only Movies+Dine-out and Movies+Dine-out and Shopping+All three)
=1200−(500+x2+x+z+y)
Substituting the known values:
=1200−(500+110+220+240+240)=1200−1110=90
Final Answer
The number of people who went for only Dine-out is 320.
- Total number of people = 2000
- Percentage of people who dined out = 60%
- Number of people who dined out = 60% of 2000 = 0.6 * 2000 = 1200
- Number of people who went shopping = 54% of 2000 = 0.54 * 2000 = 1080
- It is given that 500 people went for only shopping.
- Let:
- x = number of people who went for both Movies and Dine-out (but not shopping)
- y = number of people who went for all three activities
- z = number of people who went for both Shopping and Dine-out (but not Movies)
- The number of people who went for only Movies = x2 (half of those who went for both Movies and Dine-out).
- We know that y=z (the number of people who went for all activities is equal to those who went for both Shopping and Dine-out).
- It is also given that 100 people went for both Shopping and Movies (but not Dine-out).
- Total people who went shopping = 500 (only shopping) + 100 (shopping and movies) + z (shopping and dine-out) + y (all three activities).
- Therefore, we have:
500+100+z+y=1080
Since y=z, we can substitute y with z:
500+100+z+z=1080⟹600+2z=1080⟹2z=480⟹z=240
Thus, y=240.
- Now we can find x using the total number of people who dined out:
- Total people who dined out = 1200
- This includes:
- 500 (only dine-out)
- x (dine-out and movies)
- z=240 (dine-out and shopping)
- y=240 (all three activities)
500+x+240+240=1200⟹500+x+480=1200⟹x=1200−980=220
- Now we can find the number of people who went for only Dine-out:
Only Dine-out=Total Dine-out−(Only Shopping+Only Movies+Dine-out and Movies+Dine-out and Shopping+All three)
=1200−(500+x2+x+z+y)
Substituting the known values:
=1200−(500+110+220+240+240)=1200−1110=90
The number of people who went for only Dine-out is 320.
Similar Questions
Knowledge Check
- Question 1 - Select One
Study the following table and answer the questions.

The total number of students scoring 50% or more marks isA1250B875C775D675 - Question 2 - Select One
Study the following pie chart carefully and answer the questions. The pie chart represents the percentage of people involved in various occupations.(total number of people-20000).

How many more people are involved in service than in trade?A3360B2660C1660D660 - Question 3 - Select One
Study the following table carefully and answer the questions given below :
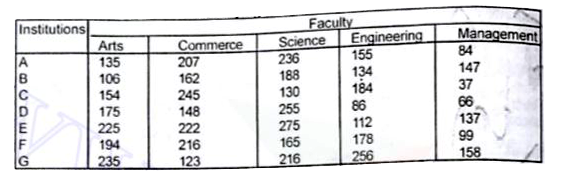
Out of the total students of the institute D, approximately what percentage of students are studying Science ?A25%B30%C45%D35%
Study the following graph carefully and answer the given questions :-
The following graph shows the % profit of two companies over the years :-
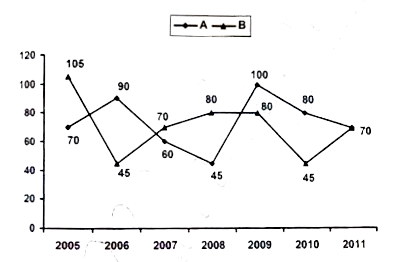
In which of the following years was the total income more than double the total expenditure in that year for company A ?View SolutionStudy the following pie chart carefully and answer the questions. The pie chart represents the percentage of people involved in various occupations.

The ratio of the people involved in service to that in industry isView SolutionStudy the following graph carefully and answer the questions given below it :-
Number of people working in various departments of two different organisation:
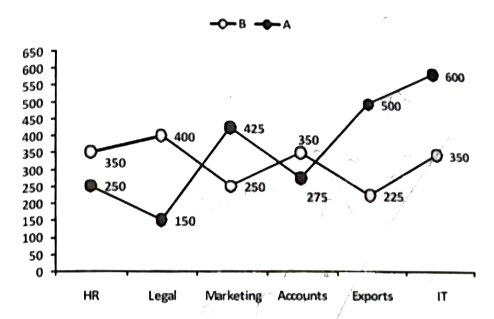
What is the total number of people working in organisation B?View SolutionStudy the following graph carefully and answer the question given below.
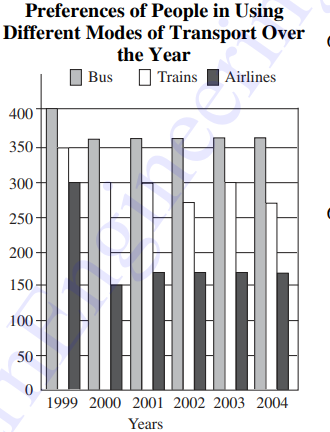 From 1999 to 2004, the total number of people who preferred to travel by trains, was approximately how many millions? View Solution
From 1999 to 2004, the total number of people who preferred to travel by trains, was approximately how many millions? View SolutionStudy the following graph carefully and answer the questions given below it :-
Number of people working in various departments of two different organisation:
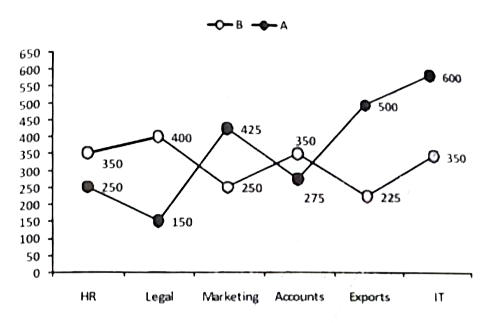
The number of people working in legal department of organisation B is approximately what percent of the total number of people working in organisation A?View Solution

