Two capacitors C1andC2 are charged to 120V and 200V, respectively. It is found that by connecting them together, the potential on each one can be made zero. Then
5C1=3C2
3C1=5C2
3C1+5C2=0
9C1=4C2
The correct Answer is:B
3C1=5C2
Explanation: V=q1−q2C1+C2
=C1V1−C2V2C1+C2
But V1=120V,V2=200V,V=0andC1+C2≠∞
C1V1−C2V2=0
C1V1=C2V2
120C1=200C2
3C1=5C2
Similar Questions
Two capacitors C1 and C2 are charged to 120V and 200V respectively. It is found that connecting them together the potential on each one can be made zero. Then
View SolutionTwo capacitors having capacitances C1 and C2 are charged with 120 V and 200 V batteries respectively. When they are connected in parallel now, it is found that the potential on each one of them is zero. Then,
View SolutionTwo capacitors having capacitances C1 and C2 are charged with 120 V and 200 V batteries respectively. When they are connected in parallel now, it is found that the potential on each one of them is zero. Then,
View SolutionTwo capacitors of 10pF and 20pF are connected to 200 V and 100 V sources, respectively. If they are connected by the wire, then what is the common potential of the capacitors?
View SolutionTwo capacitors C1 and C2 are charged 2uF AND 3uF seperately to potentials 20Vand10V, respectively. The terminals of capacitors C1andC2 are marked as (A-B) and (C-D), respectvely. A is connected with CandB is connected with D.
i. Find the final potential dsifference across each eapacitors.
ii. Find the final charge in both capacitors
iii. How much heat is produced in the circuit.
View SolutionTwo capacitors, C1andC2, charged to a potential V2 and V respectively with polarities as shown, are connected in a circuit with an ideal battery of EMF V. The capacitances are C1=2C and aC_(2)=C.Att=0, the switch S is closed. A long time after S is closed,

View SolutionTwo capacitors with capacities C1 and C2 ,are charged to potentials V1 and V2 respectively.When they are connected in parallel,the ratio of their respective charges is ....?
View SolutionTwo capacitors of 2μF and 3μF are charged to 150V and 120V, respectively. The plates of capacitor are connected as shown in the figure. An uncharged capacitor of capacity 1.5μF falls to the free end of the wire. Then
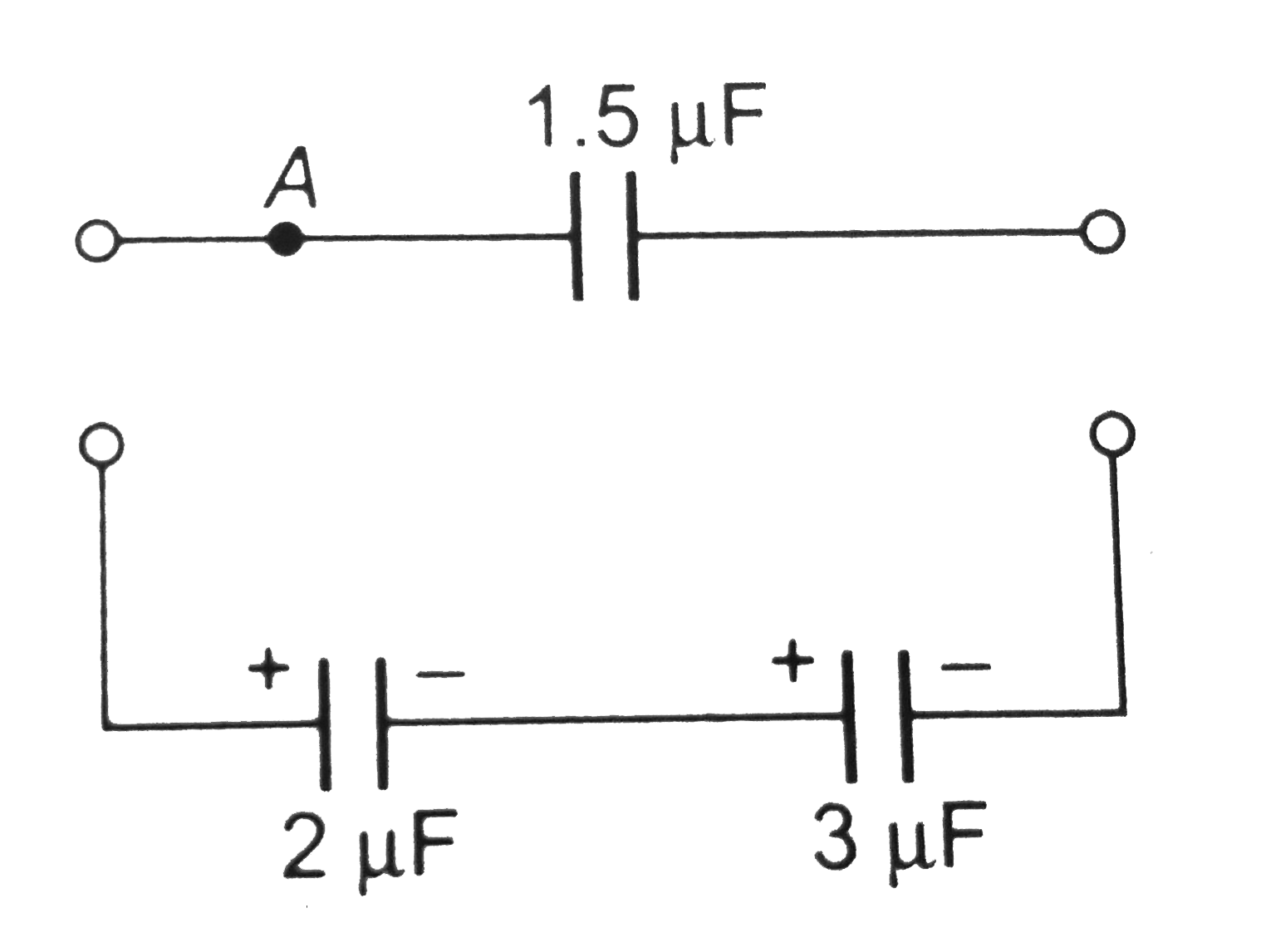
View SolutionTwo capacitors of 2μF and 3μF are charged to 150V and 120V, respectively. The plates of capacitor are connected as shown in the figure. An uncharged capacitor of capacity 1.5μF falls to the free end of the wire. Then

View SolutionTwo parallel plate condensers of capacity 20mF and 30mF are charged to the potentials of 30 V and 20 V respectively. If likely charged plates are connected together then the common potential difference be
View Solution