Two bulbs of 500 W and 250 W are manufactured to operate on a 230 V line. If their resistances are R1 and R2 respectively, then R1/R2 is:
12
2
13
15
The correct Answer is:a
To solve the problem, we need to find the equivalent resistance of two bulbs with given power ratings when connected in parallel. The power ratings of the bulbs are 500 W and 250 W, and they operate on a 230 V line.
1. Identify the given values:
- Power of the first bulb (P1) = 500 W
- Power of the second bulb (P2) = 250 W
- Voltage (V) = 230 V
2. Use the formula for resistance in terms of power:
The resistance (R) of a device can be calculated using the formula:
R=V2P
where V is the voltage and P is the power.
3. Calculate the resistance of the first bulb (R1):
R1=V2P1=(230)2500
4. Calculate the resistance of the second bulb (R2):
R2=V2P2=(230)2250
5. Find the ratio of the resistances (R1/R2):
R1R2=(230)2500(230)2250=250500=12
6. Conclusion:
The ratio of the resistances R1//R2 is 12.
Final Answer:
R1//R2=12
- Power of the first bulb (P1) = 500 W
- Power of the second bulb (P2) = 250 W
- Voltage (V) = 230 V
The resistance (R) of a device can be calculated using the formula:
R=V2P
where V is the voltage and P is the power.
R1=V2P1=(230)2500
R2=V2P2=(230)2250
R1R2=(230)2500(230)2250=250500=12
The ratio of the resistances R1//R2 is 12.
R1//R2=12
Similar Questions
Two bulbs 100W,250V and 200W,250V are connected in parallel across a 500V line. Then-
View SolutionTwo bulbs of 500 watt and 200 watt are manufactured to operate on 220 volt line. The ratio of heat produced in 500W and 200W, in two cases, when firstly they are joined in parallel and secondly in series, will be
View SolutionTwo electric bulbs , rated for the same voltage , have powers of 200Wand100W, respectively. If their resistances are r1andr2 , respectively , then
View SolutionTwo cells of emf E1=6V and E2=5 are joined in parallel with same polarity on same side without any external load. If their internal resistance are r1=2Ω and r2=3Ω respectively, then
View SolutionThree resistors R1,R2 and R3 are to be combined to form an electrical circuit as shown in the figure. It is found that when R1R2andR3 are put respectively in positions A, B and C, the effective resistance of the circuit is 70 ΩWhen R2,R3andR1 are put respectively in position A, B and C the effective resistance is 35Ω and when R3,R1andR2 are respectively put in the position A, B and C, the effective resistance is 42Ω
If R1,R2 andR3are put in series, the effective resistance will be
View SolutionThree resistors R1,R2 and R3 are to be combined to form an electrical circuit as shown in the figure. It is found that when R1R2andR3 are put respectively in positions A, B and C, the effective resistance of the circuit is 70 ΩWhen R2,R3andR1 are put respectively in position A, B and C the effective resistance is 35Ω and when R3,R1andR2 are respectively put in the position A, B and C, the effective resistance is 42Ω
If R1,R2andR3 are all connected in parallel, the effective resistance will be
View SolutionThree resistors R1,R2 and R3 are to be combined to form an electrical circuit as shown in the figure. It is found that when R1R2andR3 are put respectively in positions A, B and C, the effective resistance of the circuit is 70 ΩWhen R2,R3andR1 are put respectively in position A, B and C the effective resistance is 35Ω and when R3,R1andR2 are respectively put in the position A, B and C, the effective resistance is 42Ω
The resistanceR1:R2:R3are in the ratio
View SolutionA filament bulb (500W,100V) is to be used in a 230V main supply. When a resistance R is connected in series, it works perfectly and the bulb consumers 500W. The value of R is
View SolutionSix resistance each of value r=5Ω are connected between points A, B and C as shown in figure. If R1,R2 and R3 are the net resistance between A and B, between B and C and between A and C respectively, then R1:R2:R3 will be equal to

View SolutionThree cells of emf 3V, 4V, and 6V are connected in parallel, If their internal resistances are 1Ω, 2 Omegaand1Ω find the εeff,reff, and the current in the external load R = 1.6 Ω .
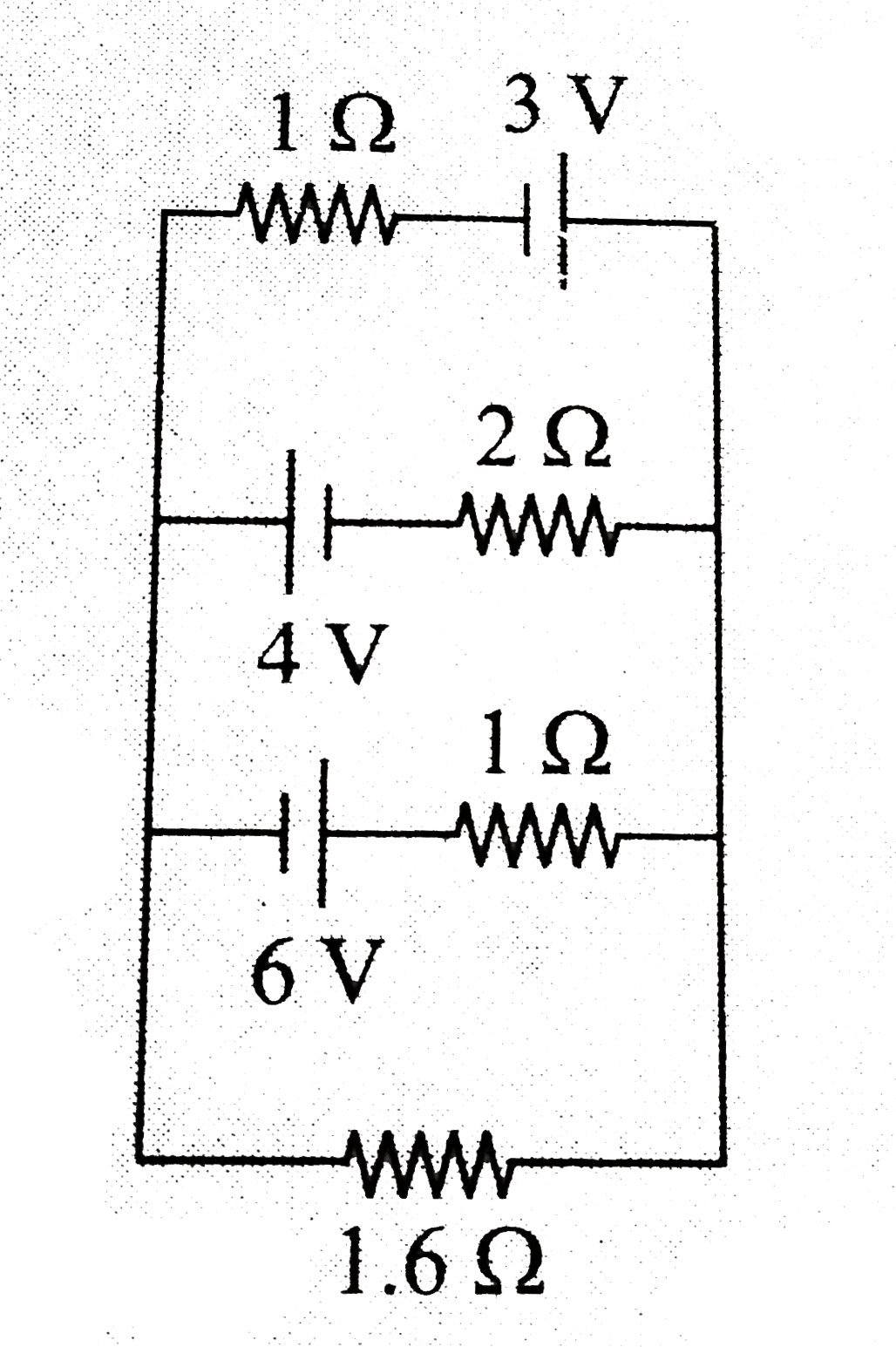
View Solution