Three resistors R1,R2 and R3 are to be combined to form an electrical circuit as shown in the figure. It is found that when R1R2andR3 are put respectively in positions A, B and C, the effective resistance of the circuit is 70 ΩWhen R2,R3andR1 are put respectively in position A, B and C the effective resistance is 35Ω and when R3,R1andR2 are respectively put in the position A, B and C, the effective resistance is 42Ω
The resistanceR1:R2:R3are in the ratio
0.04380787037037
0.043101851851852
0.043854166666667
0.043819444444444
The correct Answer is:B
To solve the problem involving the effective resistances of three resistors R1,R2, and R3 in different configurations, we can set up equations based on the information given.
1. Understanding the Problem:
We are given three configurations of resistors and their respective effective resistances:
- Configuration 1: R1,R2,R3 → Reff1=70Ω
- Configuration 2: R2,R3,R1 → Reff2=35Ω
- Configuration 3: R3,R1,R2 → Reff3=42Ω
2. Setting Up the Equations:
Let's assume that the resistors are connected in series in each configuration. The effective resistance for resistors in series is given by:
Reff=RA+RB+RC
Therefore, we can write the following equations based on the configurations:
- For Configuration 1:
R1+R2+R3=70(1)
- For Configuration 2:
R2+R3+R1=35(2)
- For Configuration 3:
R3+R1+R2=42(3)
3. Simplifying the Equations:
Notice that the equations (1), (2), and (3) are essentially the same, just rearranged. We can simplify them:
- From (1): R1+R2+R3=70
- From (2): R1+R2+R3=35
- From (3): R1+R2+R3=42
However, since they are equal, we can express them differently. Let's denote:
R1+R2+R3=S
Then we can write:
S=70(fromeq.1)
S=35(fromeq.2) (not possible)
S=42(fromeq.3) (not possible)
4. Finding Ratios:
To find the ratios of R1,R2, and R3, we can express each resistor in terms of a variable k:
R1=kx,R2=ky,R3=kz
Where x,y,z are the ratios we want to find.
From the equations, we can set up the following:
k(x+y+z)=70(4)
k(y+z+x)=35(5)
k(z+x+y)=42(6)
By dividing each equation by k, we can solve for the ratios x,y,z.
5. Solving for Ratios:
From the equations we have:
- x+y+z=70/k
- y+z+x=35/k
- z+x+y=42/k
We can equate these to find the ratios. By solving these equations, we can find the values of x,y,z that satisfy all three conditions.
6. Final Ratio:
After solving, we find that:
R1:R2:R3=2:1:3
We are given three configurations of resistors and their respective effective resistances:
- Configuration 1: R1,R2,R3 → Reff1=70Ω
- Configuration 2: R2,R3,R1 → Reff2=35Ω
- Configuration 3: R3,R1,R2 → Reff3=42Ω
Let's assume that the resistors are connected in series in each configuration. The effective resistance for resistors in series is given by:
Reff=RA+RB+RC
Therefore, we can write the following equations based on the configurations:
- For Configuration 1:
R1+R2+R3=70(1)
- For Configuration 2:
R2+R3+R1=35(2)
- For Configuration 3:
R3+R1+R2=42(3)
Notice that the equations (1), (2), and (3) are essentially the same, just rearranged. We can simplify them:
- From (1): R1+R2+R3=70
- From (2): R1+R2+R3=35
- From (3): R1+R2+R3=42
R1+R2+R3=S
Then we can write:
S=70(fromeq.1)
S=35(fromeq.2) (not possible)
S=42(fromeq.3) (not possible)
To find the ratios of R1,R2, and R3, we can express each resistor in terms of a variable k:
R1=kx,R2=ky,R3=kz
Where x,y,z are the ratios we want to find.
k(x+y+z)=70(4)
k(y+z+x)=35(5)
k(z+x+y)=42(6)
From the equations we have:
- x+y+z=70/k
- y+z+x=35/k
- z+x+y=42/k
After solving, we find that:
R1:R2:R3=2:1:3
Similar Questions
Three resistors R1,R2 and R3 are to be combined to form an electrical circuit as shown in the figure. It is found that when R1R2andR3 are put respectively in positions A, B and C, the effective resistance of the circuit is 70 ΩWhen R2,R3andR1 are put respectively in position A, B and C the effective resistance is 35Ω and when R3,R1andR2 are respectively put in the position A, B and C, the effective resistance is 42Ω
If R1,R2 andR3are put in series, the effective resistance will beView SolutionThree resistors R1,R2 and R3 are to be combined to form an electrical circuit as shown in the figure. It is found that when R1R2andR3 are put respectively in positions A, B and C, the effective resistance of the circuit is 70 ΩWhen R2,R3andR1 are put respectively in position A, B and C the effective resistance is 35Ω and when R3,R1andR2 are respectively put in the position A, B and C, the effective resistance is 42Ω
If R1,R2andR3 are all connected in parallel, the effective resistance will beView Solution
Knowledge Check
- Question 1 - Select One
In the shown in the given figure, the resistances R1andR2 are respectively
 A14Ωand40ΩB40Ωand44ΩC40Ωand30ΩD14Ωand30Ω
A14Ωand40ΩB40Ωand44ΩC40Ωand30ΩD14Ωand30Ω
In the situation shown, resistance R1,R2 and R3 are in the ratio 3:2:1 , then
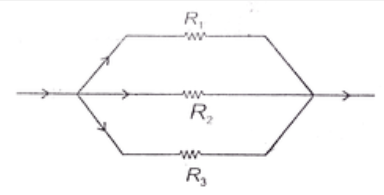 View Solution
View SolutionIn the given circuit, if I1andI2 be the current in resistances R1andR2, respectively, then
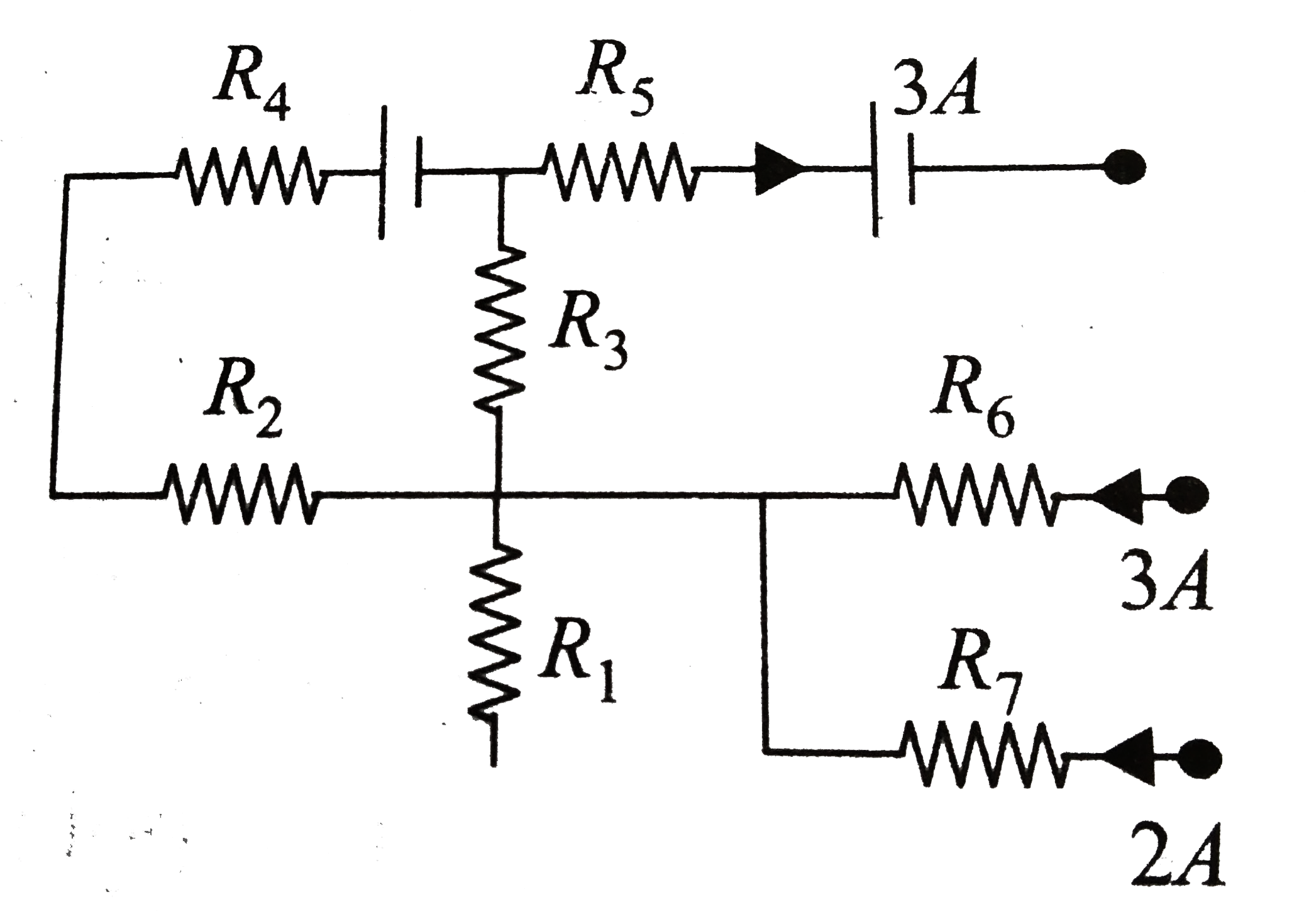 . View Solution
. View SolutionFind the currents going through the three resistors R1,R2 and R3 in the circuit of figure.
 View Solution
View SolutionConsider the circuit shown in the figure. Equivalent resistance between terminals ab,ac,c equals 30Ω,60Ω and 70Ω respectively. Find the respectively . Find the resistance R1,R2and R3
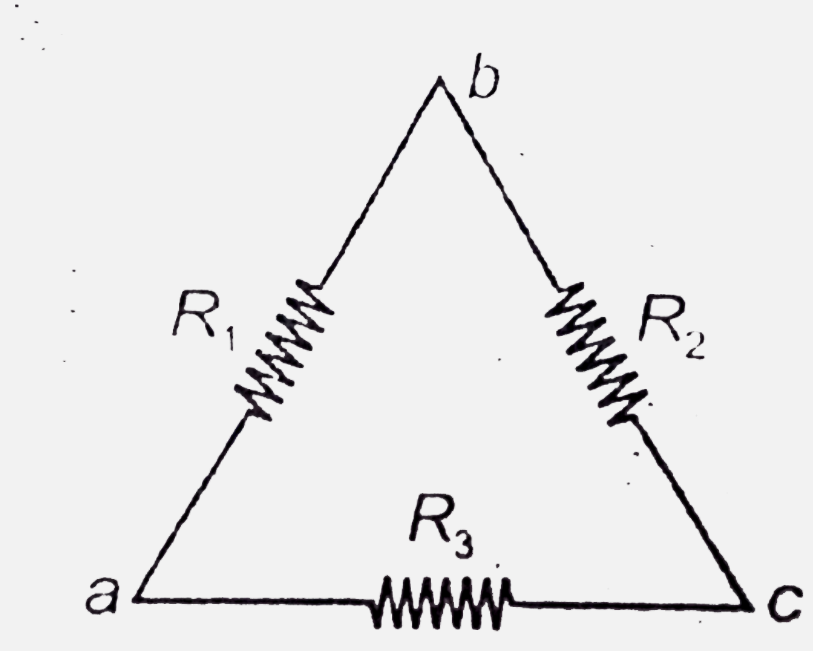 View Solution
View SolutionIn the circuit shown in figure E1=7V,E2=1V,R1=2Ω,R2=2Ω and R3=3Ω respectively. Find the power supplied by the two batteries.
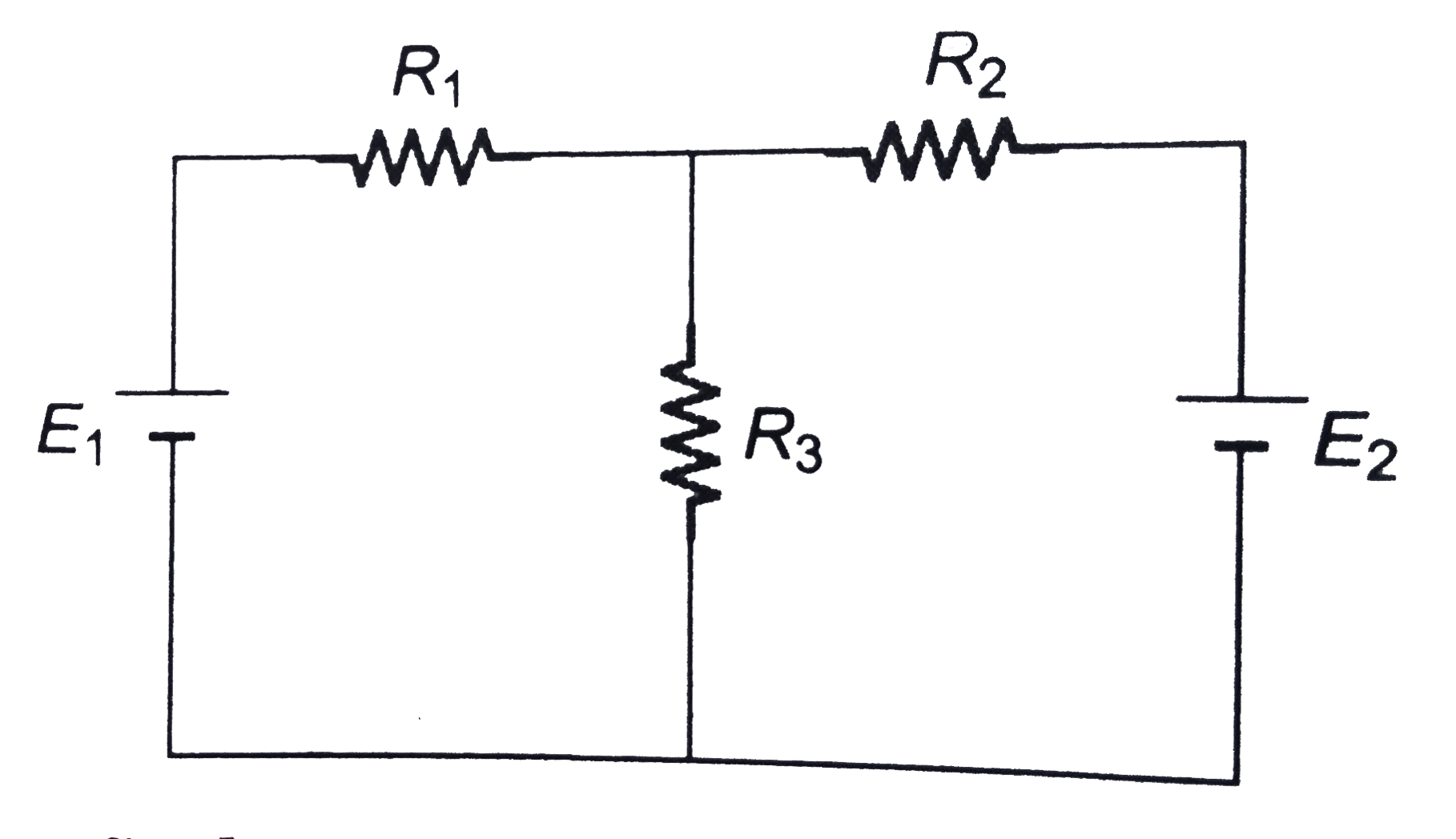 View Solution
View SolutionFigure shows three resistor configurations R1,R2 and R3 connected to 3 V battery .

If the powers dissipated by the configuration R1,R2 and R3 are P1,P2 and P3, respectively, thenView SolutionFigure shows three resistor configurations R1,R2 and R3 connected to 3 V battery .

If the powers dissipated by the configuration R1,R2 and R3 are P1,P2 and P3, respectively, thenView Solution
