Two light rays incident parallel to each other on an optical boundary will undergo the same refraction.
True
False
data is not given
none of the above
The correct Answer is:A
To solve the question, "Two light rays incident parallel to each other on an optical boundary will undergo the same refraction," we can follow these steps:
1. Understanding the Setup:
- We have two light rays that are incident parallel to each other on an optical boundary separating two media with different refractive indices, N1 and N2.
2. Identifying the Normal:
- Draw a normal line perpendicular to the optical boundary at the point of incidence. This normal line will help us measure the angles of incidence and refraction.
3. Defining Angles of Incidence:
- Let the angle of incidence for both rays be i1. Since the rays are parallel, they will make the same angle with the normal.
4. Applying Snell's Law:
- According to Snell's Law, the relationship between the angles of incidence and refraction is given by:
N1sin(i1)=N2sin(r1)
- Here, r1 is the angle of refraction for the first ray.
5. Applying Snell's Law to the Second Ray:
- For the second ray, we can similarly apply Snell's Law:
N1sin(i1)=N2sin(r2)
- Here, r2 is the angle of refraction for the second ray.
6. Equating the Two Equations:
- Since both rays have the same angle of incidence i1, we can equate the two equations:
N2sin(r1)=N2sin(r2)
7. Cancelling Out the Refractive Index:
- Assuming N2 is not zero, we can divide both sides by N2:
sin(r1)=sin(r2)
8. Concluding the Angles of Refraction:
- Since the sine function is equal, we can conclude that:
r1=r2
- Therefore, both rays undergo the same angle of refraction.
9. Final Conclusion:
- Since both rays are refracted at the same angle, they remain parallel after refraction. Thus, the statement is true.
Final Answer:
The statement "Two light rays incident parallel to each other on an optical boundary will undergo the same refraction" is True.
- We have two light rays that are incident parallel to each other on an optical boundary separating two media with different refractive indices, N1 and N2.
- Draw a normal line perpendicular to the optical boundary at the point of incidence. This normal line will help us measure the angles of incidence and refraction.
- Let the angle of incidence for both rays be i1. Since the rays are parallel, they will make the same angle with the normal.
- According to Snell's Law, the relationship between the angles of incidence and refraction is given by:
N1sin(i1)=N2sin(r1)
- Here, r1 is the angle of refraction for the first ray.
- For the second ray, we can similarly apply Snell's Law:
N1sin(i1)=N2sin(r2)
- Here, r2 is the angle of refraction for the second ray.
- Since both rays have the same angle of incidence i1, we can equate the two equations:
N2sin(r1)=N2sin(r2)
- Assuming N2 is not zero, we can divide both sides by N2:
sin(r1)=sin(r2)
- Since the sine function is equal, we can conclude that:
r1=r2
- Therefore, both rays undergo the same angle of refraction.
- Since both rays are refracted at the same angle, they remain parallel after refraction. Thus, the statement is true.
The statement "Two light rays incident parallel to each other on an optical boundary will undergo the same refraction" is True.
Topper's Solved these Questions
- REFRACTION OF LIGHTBook:ICSEChapter:REFRACTION OF LIGHTExercise:APPLICATION BASED MCQ:
Explore 17 Videos
- REFRACTION OF LIGHTBook:ICSEChapter:REFRACTION OF LIGHTExercise:NUMERICAL BASED MCQ:
Explore 6 Videos
- RADIOACTIVITYBook:ICSEChapter:RADIOACTIVITYExercise:NUMERICALS
Explore 2 Videos
- REFRACTION OF LIGHT AT PLANE SURFACESBook:ICSEChapter:REFRACTION OF LIGHT AT PLANE SURFACESExercise:EXERCISE-4(D) MULTIPLE CHOICE TYPE
Explore 3 Videos
Similar Questions
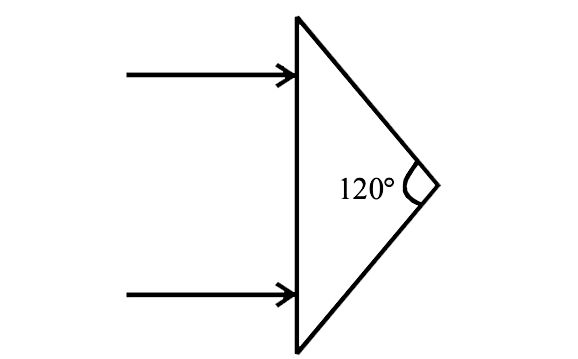
An isosceles prism of angle 120degree has a refractive index 1.44. Two parallel monochromatic rays enter the prism parallel to each other in air as shown. The rays emerge from the opposite faces
View SolutionA ray of light is incident normally on a plane glass slab. What will be (i) the angle of refraction, and (ii) the angle of deviation for the ray ?
View SolutionTwo plane mirrror are inclined to each other at 70∘. A ray of light is incident on one mirror. They ray after two reflections will undergo a total deviation of :
View SolutionTwo plane mirrors are making an angle of 60∘ to each other. A light ray falls on one of the mirrors. The light ray is incident parallel to angular bisector of mirrors. How many reflection does the light ray undergo?
View SolutionA ray of light is incident on a parallel slab of thickness t and refractive index n. If the angle of incidence θ is small, than the lateral displacement in the incident and emergent ray will be
View SolutionThe diagram below shows two parallel rays A and B of red and violet light respectively incident from air on air-glass boundary. Complete the diagram showing the refracted rays for them in the glass.
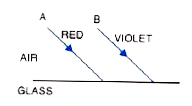
(i) How do the speeds of the rays differ in glass ?
(ii) are the two refracted rays in glass parallel ?
Give a reason for your answer.
(iii) How does the refractive index of glass differ for the two rays ?
View SolutionThe incident ray, the _______ ray and the normal lie in the same plane during refraction.
View SolutionWhen a ray of light strike the surface of seperation of two optical media _____ it does not suffer any refraction.
View SolutionA light ray is incident fromt a denser medium on the boundary separating it from a rarer medium at an angle of incidence equal to the critical angle. What is the angle of refraction for the ray ?
View SolutionA ray incident on a droplet of water from air at an angle of incidence 30∘ undergoes two reflections and emerges. If the deviation suffered by the ray is minimum then the requried refractive index of the drop μ=√x. Find the value of x.
View Solution