→E due to uniformly charged sphere of radius R as a function of distance from its centre is represented by:

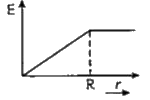

The correct Answer is:A
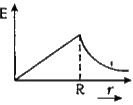
Explanation: If r<R, electric field is directly proportional to the distance from the centre and if R<r, the →E inversely proportional to the distance.
Related Playlists
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - SECTION - C6videos
SAMPLE PAPER 5
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - SECTION - C6videos
SAMPLE PAPER 5
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 3EXERCISE - SECNTION -C6videos
SAMPLE PAPER 3
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - Section-C6videos
SAMPLE PAPER 6
Similar Questions
The electric field due to uniformly charged sphere of radius R as a function of the distance from its centre is represented graphically by
View SolutionGraphical representation of electric field due to uniformly charged sphere of radius R as function of distance from its centre is given by:
View SolutionWhich of the following graph represents the variation of electric field E due to a thin charged spherical shell of radius R as a function of the distance r from the centre of the shell?
View SolutionIf the potential at the center of a uniformly charged sphere of radius R is V then electric field at a distance r from the center of sphere will be (r<R) : -
 View Solution
View SolutionIf the potential at the centre of a uniformly charged hollow sphere of radus R is V, then electric field at a distance r from the centre of sphere will be (r>R).
 View Solution
View SolutionThe electric field intensity at a distance 20cm from the centre of a uniformly charged non conducting solid sphere of radius 10cm is E.Then what is the electric field intensity at a distance 5cm from the centre it will be.....
View SolutionThe electric intensity due to a uniformly charged infinite cylinder of radius R , at a distance r(>R) , from its axis is proportional to
View SolutionA nonconducting sphere with radius a is concentric with and surrounded by a conducting spherical shell with inner radius b and outer radius c. The inner sphere has a negative charge uniformly distributed throughout its volume, while the spherical shell has no net charge. The potential V (r) as a function of distance from the center is given by
 View Solution
View SolutionThe maximum electric field intensity on the axis of a uniformly charged ring of charge q and radius R is at a distance x from the centre of the ring.The value of x is
View SolutionAssertion: Electric potential on the surface of a charged sphere of radius R is V. Then electric field at distance r=R2 from centre is V2R. Charge is distributed uniformly over the volume.
Reason: From centre to surface, electric field varies linearly with r. Here r is distance from centre.View Solution


