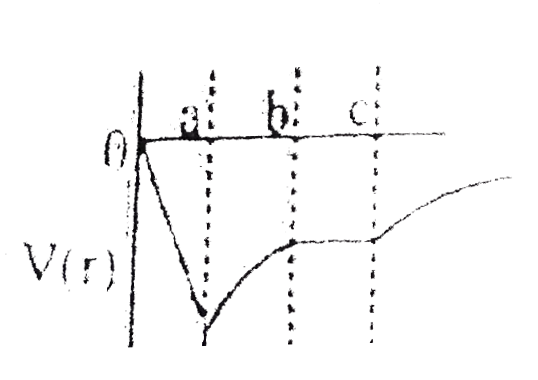
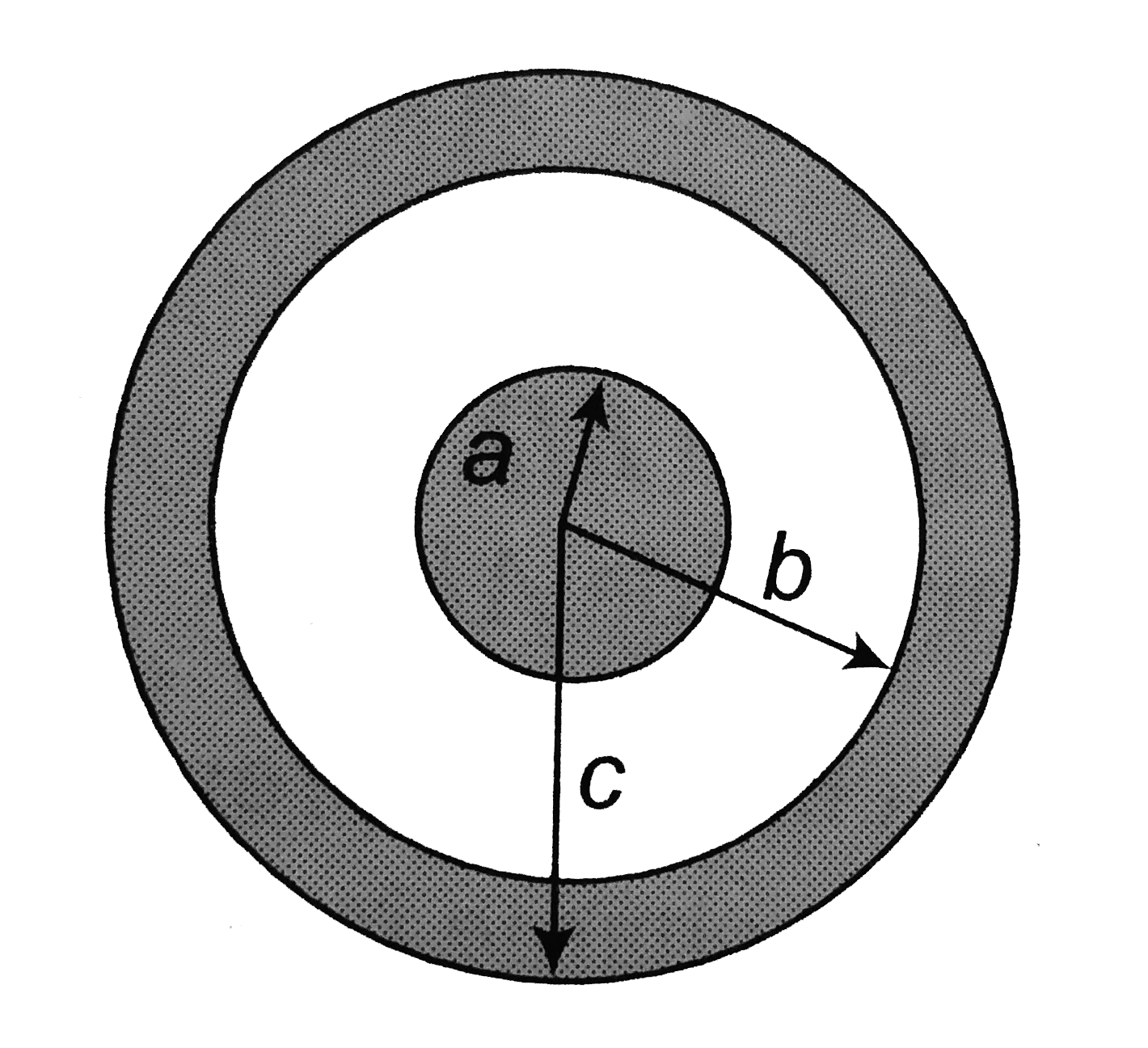
A nonconducting sphere with radius a is concentric with and surrounded by a conducting spherical shell with inner radius b and outer radius c. The inner sphere has a negative charge uniformly distributed throughout its volume, while the spherical shell has no net charge. The potential V (r) as a function of distance from the center is given by
The correct Answer is:C
for r≤a
V=KQ(3a2−r2)2a3+K(−Q)b+KQc
fora≤r≤b
V=KQr+K(−Q)b+KQc
forb≤r≤c
V=KQr+K(−Q)b+KQc=KQc
forr≤c
V=KQr+k(−Q)r+kQr=kQr
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Comphrehension
134 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning
75 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
What is the volume of the material in a spherical shell with inner radius ‘r' and outer radius 'R' ?
View SolutionA point charge +q is placed at the centre of a conducting spherical shell of inner radius a and outer radius b. Find the charge appearing on the inner and outer surface of the shell.
View Solution
Knowledge Check
A hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the
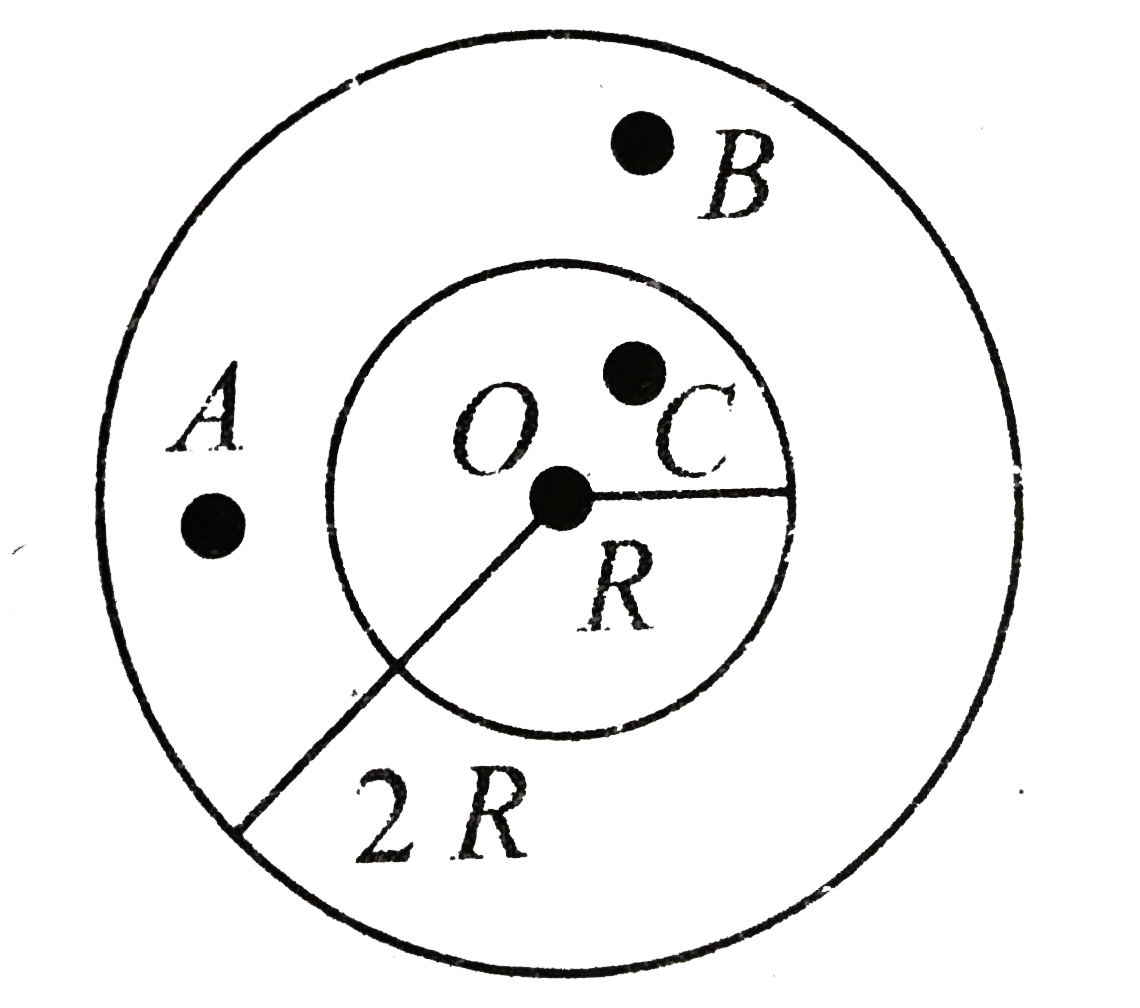Apotential at A and B is same.Bpotential at O and B is same.Cpotential at O and C is same.Dpotential at A,B,C and O is same.A solid conducting sphere of radius a has a net positive charge 2Q. A conducting spherical shell of inner radius b and outer radius c is concentric with the solid sphere and has a net charge −Q. The surface charge density on the inner and outer surfaces of the spherical shell will be
A−2Q4πb2,Q4πc2B−Q4πb2,Q4πc2C0,Q4πc2DNone of the aboveA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge +2q, and the outer shell has a total charge +4q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for
The graph of the radial component of E as a function of r will beA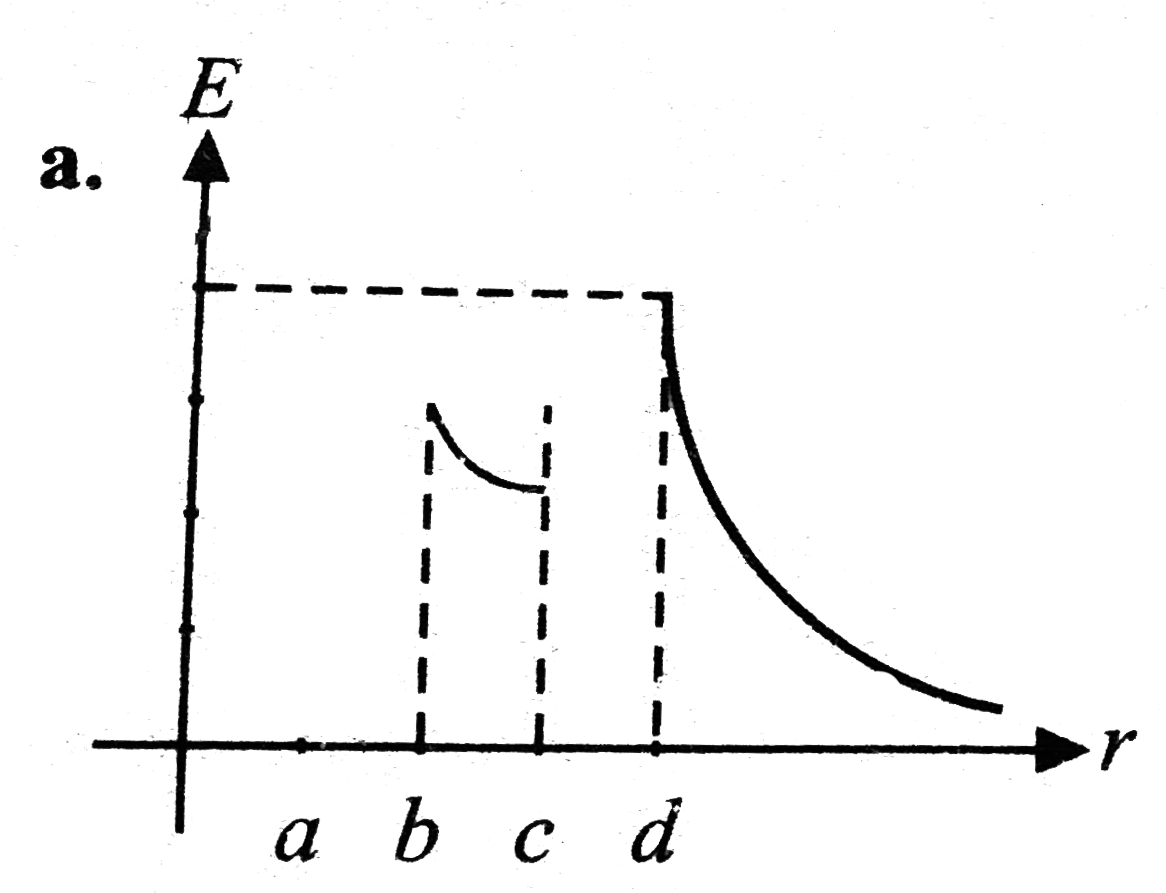
B
C
D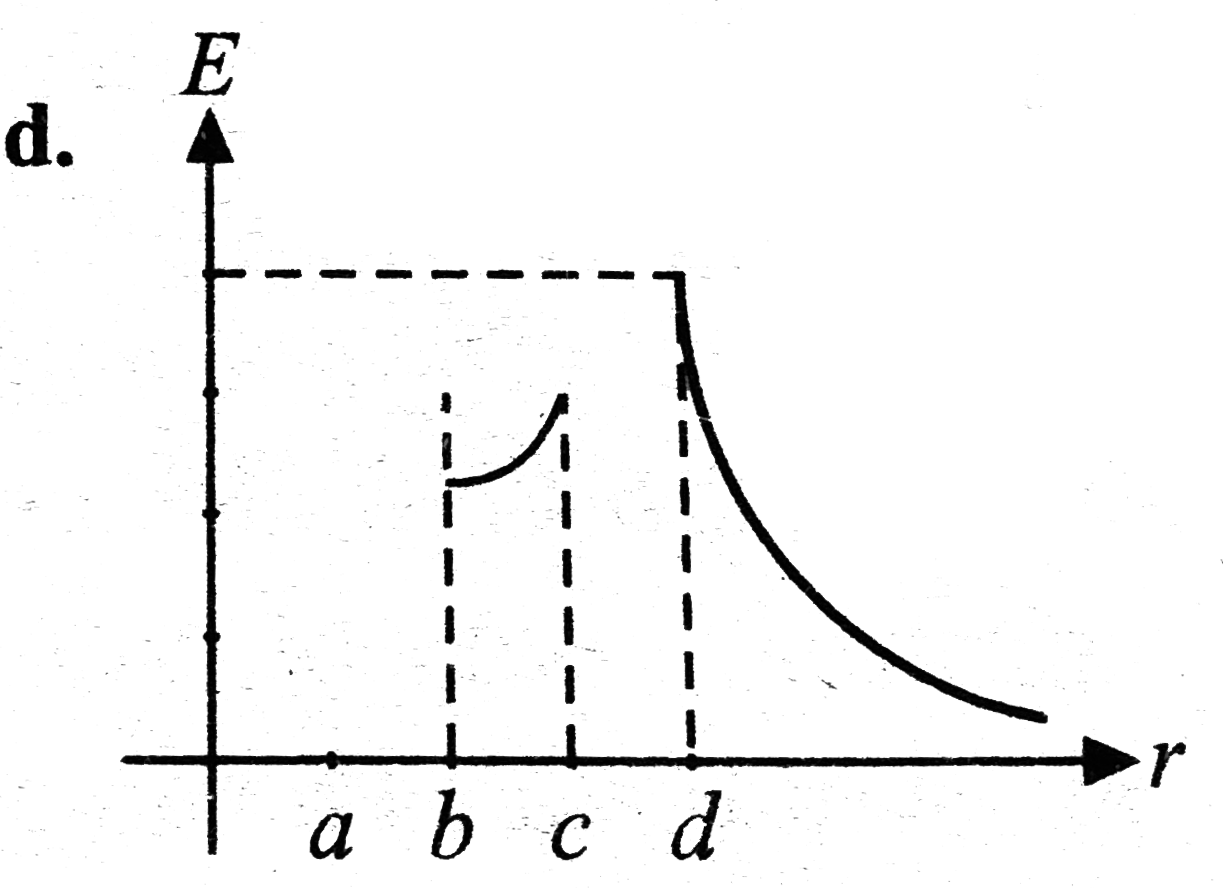
A small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge +2q, and the outer shell has a total charge +4q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for
b<r<c
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge +2q, and the outer shell has a total charge +4q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for
c<r<d
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge +2q, and the outer shell has a total charge +4q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for
a<r<b
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge +2q, and the outer shell has a total charge +4q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for
r<a
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge +2q, and the outer shell has a total charge +4q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for
r>d
View Solution