ΔPQR and ΔTQR are on the same base QR and on the same side of QR, If PQ=TR and PR=TQ, then which of the following is correct?
ΔPQR≅ΔRQT
ΔPQR≅ΔQTR
ΔPQR≅ΔTQR
ΔPQR≅ΔTRQ
The correct Answer is:D
To solve the problem, we need to analyze the given information about triangles ΔPQR and ΔTQR.
Step 1: Understand the Given Information
We have two triangles, ΔPQR and ΔTQR, which share a common base QR and are located on the same side of this base. The information provided states:
- PQ=TR
- PR=TQ
Step 2: Identify the Corresponding Sides
From the information:
- Side PQ of triangle PQR is equal to side TR of triangle TQR.
- Side PR of triangle PQR is equal to side TQ of triangle TQR.
- The base QR is common to both triangles.
Step 3: Apply the Side-Side-Side (SSS) Congruence Criterion
Since we have:
- PQ=TR
- PR=TQ
- QR=QR (common side)
We can conclude that both triangles ΔPQR and ΔTQR are congruent by the Side-Side-Side (SSS) congruence criterion.
Step 4: Conclusion
Since the two triangles are congruent, we can state that:
- ΔPQR≅ΔTQR
Now, we can check the options provided in the question to identify which condition is correct based on the congruence of the triangles.
Final Answer
The correct option is Option 4: ΔPQR≅ΔTQR.
---
We have two triangles, ΔPQR and ΔTQR, which share a common base QR and are located on the same side of this base. The information provided states:
- PQ=TR
- PR=TQ
From the information:
- Side PQ of triangle PQR is equal to side TR of triangle TQR.
- Side PR of triangle PQR is equal to side TQ of triangle TQR.
- The base QR is common to both triangles.
Since we have:
- PQ=TR
- PR=TQ
- QR=QR (common side)
Since the two triangles are congruent, we can state that:
- ΔPQR≅ΔTQR
The correct option is Option 4: ΔPQR≅ΔTQR.
Similar Questions
Knowledge Check
ΔPQRandΔTQR are on the same base QR and on the same side of QR . If PQ = TR and PR = TQ, then which of the following is correct ?
AΔPQR≅ΔTQRBΔPQR≅ΔTRQCΔPQR≅ΔRQRDΔPQR≅ΔQTRIn ΔPQR,PQ=4cm,PR=6cmandQR=3cm. Which of the following is correct?
A<Q=<RB<R<<PC<R><QD<Q><RIn ΔPQR,PQ=4cm,PR=6cmandQR=3cm. Which of the following is correct?
A∠Q=∠RB∠R<∠PC∠R>∠QD∠Q>∠R
In the figure, in ΔPQRandΔTQR,PQ=TRandPR=TQ. Which of the following statements is true?
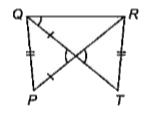
View SolutionIn ΔPQR,PQ=4 cm, PR = 6 cm and QR = 3 cm . Which of the following is correct ?
View SolutionIn the figure, in triangles PQR and TQR , PQ = TR and PR = TQ . Which of the following statements is true ?
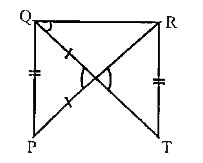
View SolutionIn the figure, in ΔPQR and ΔTQR PQ = TR and PR = TQ.
Which of the following statements is true?

View SolutionIf S is any point on the side QR of a ΔPQR, then
View Solution
