The figure shows the variation of force acting on a particle of mass 400 g executing simple harmonic motion. The
frequency of oscillation of the particle is
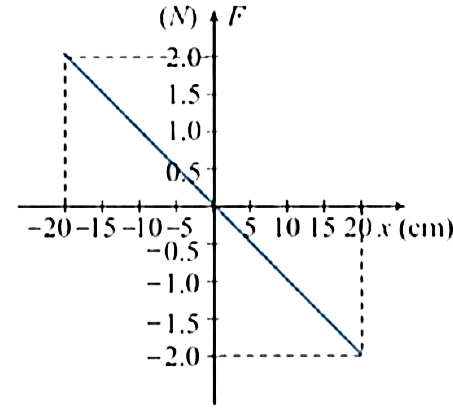
A
4s−1
B
(5/2π)s−1
C
(1/8π)s−1
D
(1/2π)s−1
Video Solution
Text Solution
The correct Answer is:B
The slope of the curve is
Fx=−0.55=−0.1Ncm=−10N/m But F =- mω2x or F/x=−mω2 so, −mω2=−10orω2=10m
∴ω2=104×10−1⇒ω=102=5 ∴f=ω2π=52π8−1
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
While a particle executes linear simple harmonic motion
Aits linear velocity and acceleration pass through their maximum and minimum values once in each oscillation.BIts linear velocity and acceleration pass through their maximum and minimum values twice in each oscillation.Cits linear velocity and acceleration pass through their maximum and minimum values four times in each oscillation.Dits linear velocity and acceleration always attain their peak values simlataneaously.The velocity of a particle executing simple harmonic motion is
Aω2√A2+x2Bω√A2−x2Cω√A2+x2Dω2√A2−x2If a particle is executing simple harmonic motion, then acceleration of particle
Ais uniformBvaries linearly with timeCis non uniformDBoth (2) & (3)
" The frequency of a particle executing simple harmonic motion is 'f' hertz.The frequency of variation of its kinetic energy is "
View SolutionThe resultant force acting on a particle executing simple harmonic motion is 4N when it is 5cm away from the centre of oscillation. Find the spring constant.
View SolutionThe acceleration-displacement graph of a particle executing simple harmonic motion is shown in the figure. The frequency of oscillation is
View SolutionIn simple harmonic motion,the particle is
View SolutionThe phase of a particle executing simple harmonic motion is π2 when it has
View Solution


