Two resistors of resistance 2 ohm and 4 ohm when connected to a battery will have
same current flowing through them when connected in parallel.
same current flowing through them when connected in series.
same potential difference across them when connected in series.
same potential difference across them when connected in series.
The correct Answer is:B
To solve the question regarding the two resistors of resistance 2 ohm and 4 ohm when connected to a battery, we need to analyze their behavior in both series and parallel configurations.
1. Identify the Configuration:
We have two resistors: R1 = 2 ohms and R2 = 4 ohms. We will analyze both series and parallel connections.
2. Series Connection:
- In a series connection, the total resistance (R_total) is the sum of the individual resistances.
- Formula:
Rtotal(series)=R1+R2=2Ω+4Ω=6Ω
- In a series circuit, the same current flows through both resistors.
3. Parallel Connection:
- In a parallel connection, the total resistance (R_total) can be calculated using the formula:
1Rtotal(parallel)=1R1+1R2=12Ω+14Ω
- Finding a common denominator (which is 4):
1Rtotal(parallel)=24+14=34
- Thus, the total resistance in parallel is:
Rtotal(parallel)=43Ω≈1.33Ω
- In a parallel circuit, the potential difference (voltage) across each resistor is the same.
4. Summary of Findings:
- In series:
- Total resistance = 6 ohms
- Same current flows through both resistors.
- In parallel:
- Total resistance = 1.33 ohms
- Same potential difference across both resistors.
Conclusion:
When connected to a battery:
- In series, the current is the same through both resistors, but the total resistance is 6 ohms.
- In parallel, the potential difference is the same across both resistors, but the total resistance is approximately 1.33 ohms.
We have two resistors: R1 = 2 ohms and R2 = 4 ohms. We will analyze both series and parallel connections.
- In a series connection, the total resistance (R_total) is the sum of the individual resistances.
- Formula:
Rtotal(series)=R1+R2=2Ω+4Ω=6Ω
- In a series circuit, the same current flows through both resistors.
- In a parallel connection, the total resistance (R_total) can be calculated using the formula:
1Rtotal(parallel)=1R1+1R2=12Ω+14Ω
- Finding a common denominator (which is 4):
1Rtotal(parallel)=24+14=34
- Thus, the total resistance in parallel is:
Rtotal(parallel)=43Ω≈1.33Ω
- In a parallel circuit, the potential difference (voltage) across each resistor is the same.
- In series:
- Total resistance = 6 ohms
- Same current flows through both resistors.
- In parallel:
- Total resistance = 1.33 ohms
- Same potential difference across both resistors.
When connected to a battery:
- In series, the current is the same through both resistors, but the total resistance is 6 ohms.
- In parallel, the potential difference is the same across both resistors, but the total resistance is approximately 1.33 ohms.
Similar Questions
Knowledge Check
Two resistors of resistances 2Ωand4Ω when connected to a battery will have :
Asame current flowing through them when connected in parallelBsame current flowing through them when connected in seriesCsame potential difference across them when connected in seriesDdifferent potential differences across them when connected in parallel.A potentiometer wire 10 m long has a resistance 40ohms. It is put in series to a resistance 760ohms and connected to a 2volt battery. The potential gradient in the wire is –
A1×10−6V/mB1×10−4V/mC1×10−3V/mD1×10−2V/mThree resistances of magnitude 2, 3 and 5 ohm are connected in parallel to a battery of 10 volts and of negligible resistance. The potential difference across 3Ω resistance will be
A2 voltsB3 voltsC5 voltsD10 volts
Two batteries (connected in series) of same emf 10 V of internal resistances 20ohm and 5ohm are connected to a load resistance of 30ohm. Now an unknown resistance x is connected in parallel to the load resistance. Find value of x so that potential drop of battery having internal resistance 20ohm becomes zero.
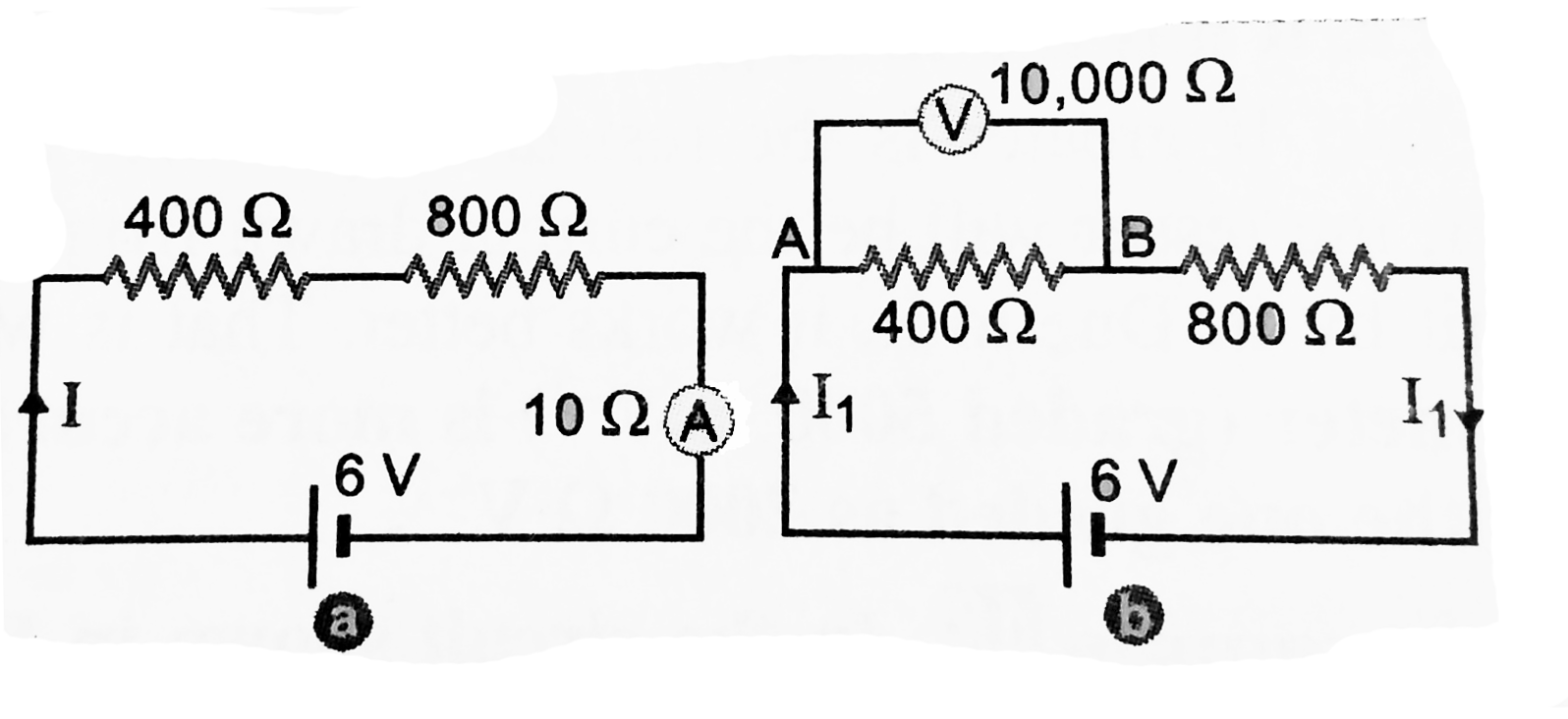
View SolutionTwo resistors 400Ω and 800Ω are connected in series with a 6V battery. It is desired to measure the current in the circuit. An ammeter of 10Ω resistance is used for this purpose figure. What will be the reading in the ammeter? Similarly, if a voltmeter of 10,000Ω resistance is used to measure the potential difference across the 400Ω resistor, what will be the reading in the voltmeter?
View SolutionTwo identical resistors, each of resistance 15ohm are connected in (i) series and (ii) parallel, in turn to battery of 6V. Calculate the ratio of the power consumed in the combination of resistors in each case.
View SolutionA silver voltameter of resistance 2 ohm and a 3 ohm resistor are connected in series across a cell. If a resistance of 2 ohm is connected in parallel with the voltameter, then the rate of deposition of silver
View SolutionTwo resistances 300 ohm and 400 ohm are connected in series with a 60 volt supply. voltmeter connected across 400 ohm reads 30V. The same voltmeter when connected across the other resistance will read.
View Solution
