Two identical resistors of resistance 100±5 ohm are connected parallel. Calculate the eqivalent resistance of the combination.
To solve the problem of finding the equivalent resistance of two identical resistors connected in parallel, we can follow these steps:
Step 1: Identify the Resistance Values
We have two identical resistors, each with a resistance of R=100±5 ohms. This means that the resistance of each resistor can vary between 95 ohms and 105 ohms.
Step 2: Use the Formula for Equivalent Resistance in Parallel
The formula for the equivalent resistance Req of two resistors R1 and R2 connected in parallel is given by:
1Req=1R1+1R2
Since both resistors are identical, we can simplify this to:
1Req=1R+1R=2R
Step 3: Calculate the Equivalent Resistance
From the above equation, we can express Req as:
Req=R2
Substituting the value of R:
Req=100ohms2=50ohms
Step 4: Calculate the Uncertainty in Equivalent Resistance
To find the uncertainty in the equivalent resistance, we can use the formula for the propagation of uncertainty in parallel resistors. The uncertainty in Req can be calculated using:
ΔReq=R2eq(ΔR1R21+ΔR2R22)
Since R1=R2=R, we can simplify this to:
ΔReq=R2eq(2⋅ΔRR2)
Substituting the values:
- Req=50ohms
- ΔR=5ohms
- R=100ohms
ΔReq=502(2⋅51002)
Calculating this gives:
ΔReq=2500(2⋅510000)=2500⋅1010000=2500⋅0.001=2.5ohms
Final Result
Thus, the equivalent resistance of the combination is:
Req=50±2.5ohms
We have two identical resistors, each with a resistance of R=100±5 ohms. This means that the resistance of each resistor can vary between 95 ohms and 105 ohms.
The formula for the equivalent resistance Req of two resistors R1 and R2 connected in parallel is given by:
From the above equation, we can express Req as:
To find the uncertainty in the equivalent resistance, we can use the formula for the propagation of uncertainty in parallel resistors. The uncertainty in Req can be calculated using:
- ΔR=5ohms
- R=100ohms
Thus, the equivalent resistance of the combination is:
Topper's Solved these Questions
- UNITS AND MEASUREMENTBOOK - MODERN PUBLICATIONCHAPTER - UNITS AND MEASUREMENTEXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS) (MCQs)
20 Videos
- UNITS AND MEASUREMENTBOOK - MODERN PUBLICATIONCHAPTER - UNITS AND MEASUREMENTEXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS) (MCQs) (AIPMT/NEET OTHER STATE BOARDS FOR MEDICAL ENTRANCE)
37 Videos
- UNITS AND MEASUREMENTBOOK - MODERN PUBLICATIONCHAPTER - UNITS AND MEASUREMENTEXERCISE - REVISION EXERCISES (LONG ANSWER QUESTIONS)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
- WAVESBOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
Two identical resistors of resiatance (2±0.1)Ω are connected in series. Calculate the effective resistance along with the percentage error.
View SolutionEstablish a relationship to determine the equivalent resistance R of a combination of three resistors having resistances R1,R2andR3 connected in series.
(b) Calculate the equivalent resistance R of a combination of three resistors of 2Ω,3Ωand6Ω joined in parallel.
View Solution
Knowledge Check
The resistors of resistances 2Ω,4Ω and 8Ω are connected in parallel, then the equivalent resistance of the combination will be
A87ΩB78ΩC74ΩD49ΩThree identical resistors, each of 6Ω are connected in parallel. The equivalent resistance of the combination will be ______.
A6ΩB18ΩC2ΩD3ΩIf three resistors of resistance 2Ω,4Ω and 5Ω are connected in parallel then the total resistance of the combination will be
A2019ΩB1920ΩC1910ΩD1019Ω
If resistors of resistance R1 and R2 are connected in parallel,then resultant resistance is "
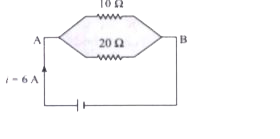
View SolutionTwo resistors of resistance 10Ω and 20Ω are connected in parallel. A battery supplies 6 A of current to the combination. Calculate the current in each resistor.
View SolutionIf 3 resistances of 3 ohm each are connected in parallel, what will be their total resistance?
View SolutionIf 'n' number of identical resistors are connected oin parallel combination, then the effective resistance of thec combination is ______.
View SolutionThree resistors with magnitudes 2,4 and 8 ohm are connected in parallel. The equivalent resistance of the system would be
View Solution
