A particle is kept at rest at the origin. A constant force → F starts acting on it at t=0. Find the speed of the particle at time t. Solution in Gujrati
The equation of motion is . →dpdt=→F
As the particle starts from rest and the force is always in the same direction, the motion will be along this direction , Thus, we can write dpdt=F
or, (∫P0dp=∫t0Fdt)
p=Ft
or, m0V√1−v2c2=Ft
or, m20V2=F2t2−F2t2C2V2
V^(2) (m_(0)^(2) + F^(2) t^(2) / C^(2)) = F^(2) t^(2)<br>or,V = Ftc / (sqrt m_(0) ^(2) C^(2) + F^(2) t^(2))
Note from example (47.4) that however large t may be , V can never exceed c, No matter how long you apply a force , the speed of a particl will be less than the speed c.
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - THE SPECIAL THEORY OF RELATIVITYEXERCISE - worked out example8videos
THE SPECIAL THEORY OF RELATIVITY
- BOOK - HC VERMACHAPTER - THE SPECIAL THEORY OF RELATIVITYEXERCISE - Short answer5videos
THE SPECIAL THEORY OF RELATIVITY
- BOOK - HC VERMACHAPTER - THE NUCLEOUSEXERCISE - Exercises53videos
THE NUCLEOUS
- BOOK - HC VERMACHAPTER - THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTEXERCISE - Exercises24videos
THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENT
Similar Questions
A hypothetical train moving with a speed of 0.6 c passes by the platform of a small station without being slowed down. The observes o the platform note that the length of the train is just equal to the length of the platform which is 200 m . (a) Find the rest length of the train (b) Find the length of the platform as measured by the obsevers in the train .
View SolutionThe speed of light in glass is 2.0×108ms−1. Does it violate the second postulate of special relativity ?
View SolutionAssume that the mass of a nucleus is approximately given by M=Ampwhere A is the mass number.Estimate the density of matter in kgm−3inside a nucleus.
01:57View SolutionAn electric current of 2.0 A passes through a wire of resistance 25Ω. How much heat will be developed in 1 minute?
View SolutionA particle is kept at rest at the origin. A constant force → F starts acting on it at t=0. Find the speed of the particle at time t.
07:11View SolutionA particle of rest mass m0 starts moving at a moment t=0 due to a constant force F. Find the time dependence of the particle's velocity and of the distance covered.
03:15View SolutionForce acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K//V K is constant then speed of the particle in time t
02:11View SolutionA particle initially at rest on a smooth horizontal surface, is acted on by a constant horizontal force at time t=0 then if W= work, done t=time and v=speed of the particle, the nearly correct graph (s) is //are
01:14View SolutionAt the moment t = 0 a stationary particle of mass m experiences a time-dependent force F = kt(t'-t) ,where is a constant vector, t' is the time during which the given force acts. Find : (a) The momentum of the particle when the action of the force discontinued, (b) The distance covered by particle while the force acted.
03:36View SolutionA particle is resting over a smooth horizontal floor AT t = 0, a horizontal force starts acting on it. Magnitude of the force increases with time F = kt, where k is a constant. The two curves are drawn for this particle as shown
View SolutionA graph of acceleration versus time of a particle starting from rest at t=0 is as shown in figure. The speed of the particle at t = 14s is
03:42View SolutionA particle of mass m is acted upon by a force F= t^2-kx . Initially , the particle is at rest at the origin. Then
02:19View SolutionA particle is kept at rest at the origin. A constant force →F starts acting on it at t=0. Find the speed of the particle at time t.
02:49View SolutionA graph of acceleration versus time of a particle starting from rest at t =0 is shown. The speed of the particle at t=14 second is
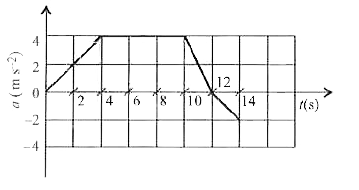 01:52View Solution
01:52View SolutionA block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
03:42View SolutionForce acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K//V K is constant then speed of the particle in time t
01:06View Solution
