Shows two long metal rails placed horizontally and parallel to each other at a separation i. A uniform magnetic field b exists in the vertically downward direction. A wire of mass m can slide on the rails. The rails are connected to a constant current source which drives a current I in the circuirt. The friction coefficient between the rails and the wire is μ. (a) What should be the minimum value of μ which can prevent the wire from sliding on the rails? (b) Describe the motion of the wire if the value of μ is half the value found in the previous part.
 Solution in Gujrati
Solution in Gujrati
(a)The force on the wire due to the magnetic field is
→F=i→l×→B
or, F=ilB.
it acts towards right in the given figure. If the wire dose not slide on the rails, the force of freiction by the rails should be equal to F. If μ0 mg thus, μ0mg=ilB or, μ0=ilBmg (b) If the friction coefficient is μ=μ02=ilB2mg,thewirewillsl→wardsright.Theictionalforcebytherailsisf=mumg= (ilB)/(2)→wards≤ft.Therestant–––––forceisilB - (ilB)/(2)= (ilB)/(2)→wardsright.theae≤rationwillbea = (ilB)/(2) = (ilB)/(2)→wardsright.theae≤rationwillbea = (ilB)/(2m). The wire will slide towards right with this acceleration.
Topper's Solved these Questions
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Short Answer
10 Videos
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Objective 1
10 Videos
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Exercises
61 Videos
- LIGHT WAVESBOOK - HC VERMACHAPTER - LIGHT WAVESEXERCISE - Exercises
41 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Exercises
61 Videos
Similar Questions
Suppose a charged particle moves with a velocity v near a wire carrying an electric current. A magnetic force, therefore, acts on it. If the same particle is seen form a frame moving with velocity v in the same direction the charge will be found at rest. Will the magnetic force become zero in this frame? Will the magnetic field become zero in this frame?
View SolutionA positively charged particle projected towards east is deflected towards north by a magnetic field. The field may be
View SolutionAn alpha particle is projected vertically upward a speed of 3.0X104kms−1 in a region where a magnetic field of magnitude 1.0 T exists in the direction south to north. Find the magnetic force that acts on the a particle.
View SolutionFind the range of frequency of light that is visible to an average human being (400nm<λ<700nm)
View SolutionUsing the formulae ((→F)=(→qv)×(→B)and(B=(μ0)i2πr), show that the SI units of the magnetic field B and the permeability constant (μ0) may be written as (NmA−1) and (NA−2) respectively.
View SolutionShows two long metal rails placed horizontally and parallel to each other at a separation i. A uniform magnetic field b exists in the vertically downward direction. A wire of mass m can slide on the rails. The rails are connected to a constant current source which drives a current I in the circuirt. The friction coefficient between the rails and the wire is mu . (a) What should be the minimum value of mu which can prevent the wire from sliding on the rails? (b) Describe the motion of the wire if the value of mu is half the value found in the previous part.
View SolutionA straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is μ. If the wire carries a current I, what minimum magnetic field should exist in the space in order to slide the wire on the rails.
View SolutionA metal wire PQ of mass 10g lies at rest on two horizontal metal rails separated by 5cm as shown in Fig. A vertically downward magnetic field of magnitude 0.80T exist in the space. The resistance of the circuit is slowly decreased and it is found that when the resistance goes below 20.0Omega the wire PQ starts sliding on the rails. The coefficient of friction between wires and rails is found. The coefficient of friction between wires and rails is found to be n//25 . find n
View SolutionA metal wire of mass m slides without friction on two horizontal rails spaced distance d-apart as shown in figure. The rails are situated in a uniform magnetic field B, directed vertically upwards, and a battery is sending a current I through them. Find the velocity of the wire as a function of time, assuming it to be at rest initially.
View SolutionFigure shows a wire sliding on two parallel, conducting rails placed at a separation L . A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity V ?
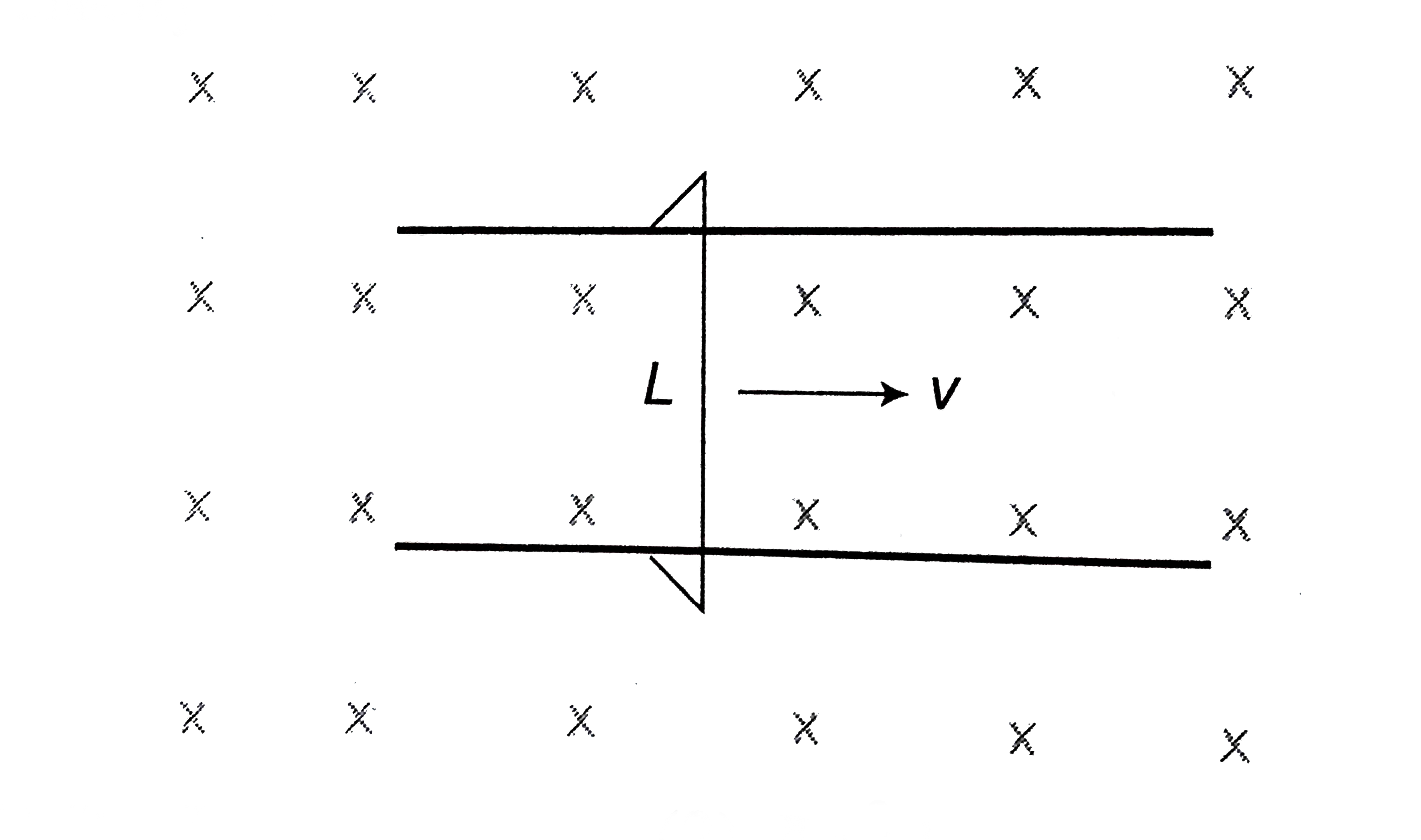
View SolutionIn a metal wire of mass m=24.1 mg can slide with negligible friction on two horizontal parallel rails separated by distance d=2.56 cm . The track lies in a vertical uniform magnetic field of magnitude 56.3 m. At time t=0 , device G is connected to the rails . producing a constant current i=9.13 mA in the wire and rails (even as the wire moves). At t=61.1 ms , what are the wire's (a) speed and (b) direction of motion (left or right)?
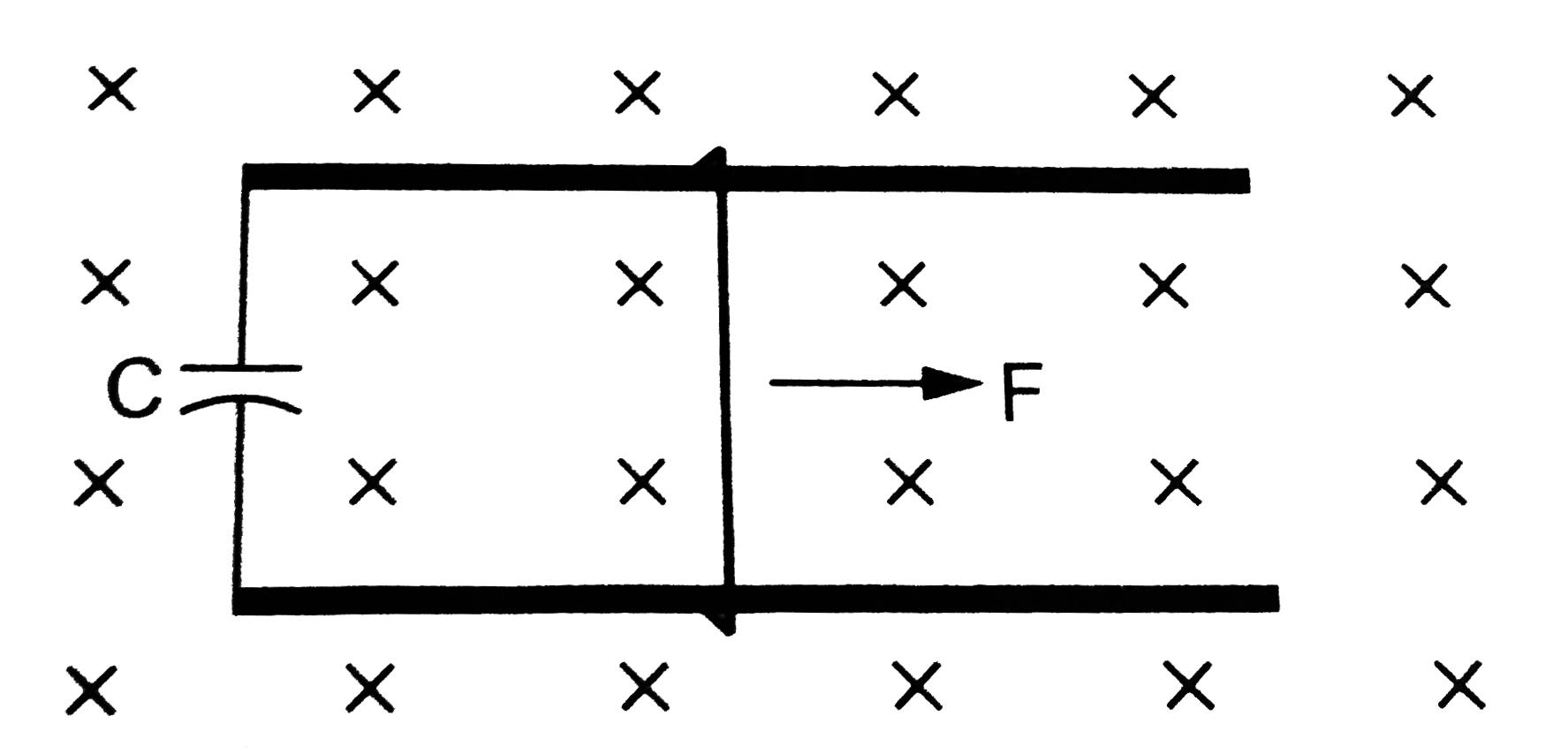
View SolutionA wire having mass m and length 1 can freely slide on a pair or parallel smooth horizontal rails placed in vertical magnetic field B. The rails are connected by a capacitor of capacitance C . The electric resistance of the rails and the wire is zero .If a constant force F acts on the Wire as shown in the figure . Then ,the acceleration of the wire can be given as

View SolutionShows two long metal rails placed horizontally and parallel to each other at a separation i. A uniform magnetic field b exists in the vertically downward direction. A wire of mass m can slide on the rails. The rails are connected to a constant current source which drives a current I in the circuirt. The friction coefficient between the rails and the wire is μ. (a) What should be the minimum value of μ which can prevent the wire from sliding on the rails? (b) Describe the motion of the wire if the value of μ is half the value found in the previous part.

View SolutionA straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is μ. If the wire carries a current I, what minimum magnetic field should exist in the space in order to slide the wire on the rails.
View SolutionA wire of mass m and length I can freely slide on a pair of parallel, smooth, horizontal rails placed in a vertical magnetic field B . The rails are connected by a capacitor of capacitance C. The electric resistance of the rails and the wire is zero. If a constant force F acts on the wire as shown in the figure, find the acceleration of the wire.
View SolutionFigure shows a wire sliding on two parallel, conducting rails placed at a separation L . A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity V ?

View Solution
