_E01_210_Q01.png)
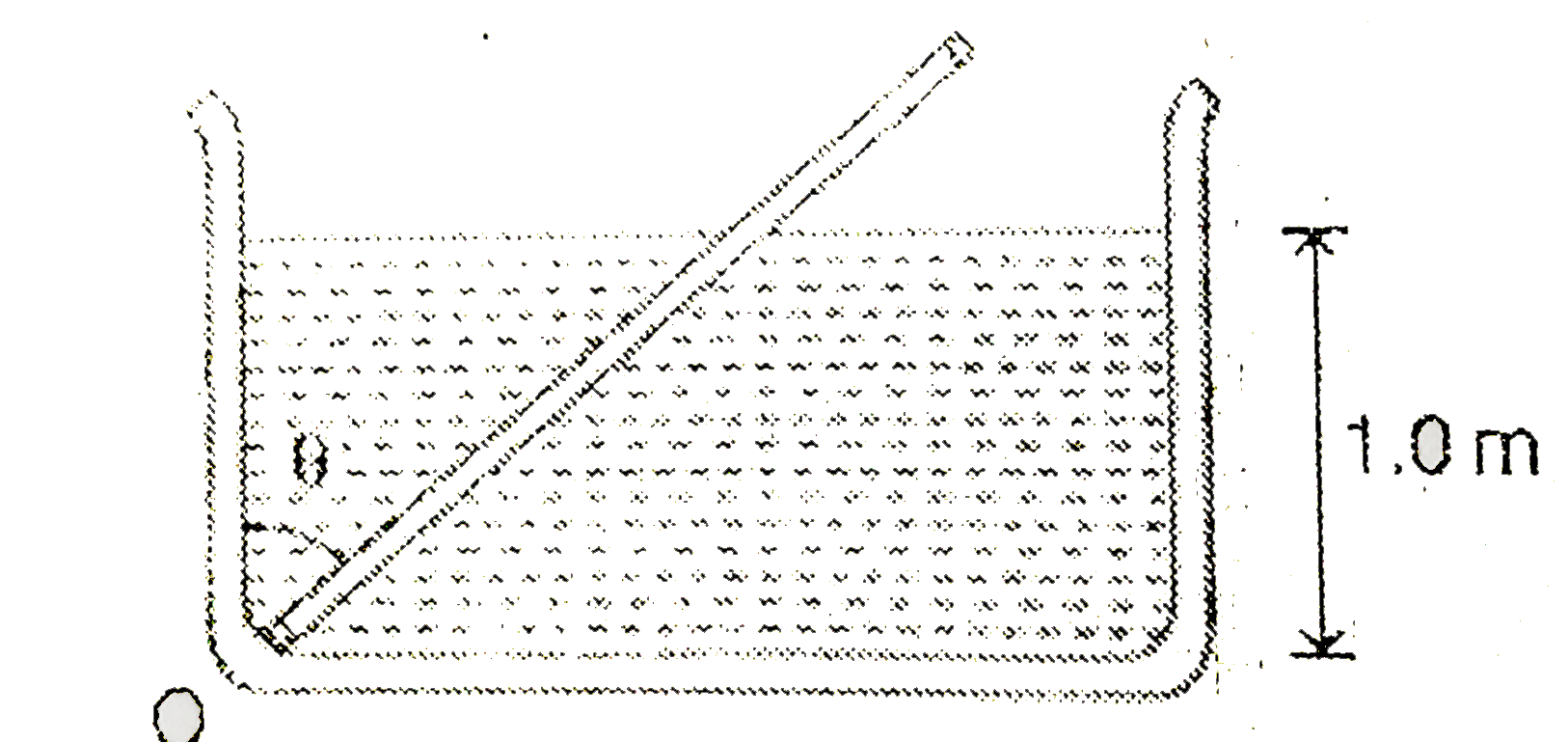
A wooded plank of length 1m and uniform cross-section is hinged at one end to the bottom of a tank as shown in figure tank is filled with water upto a height 0.5m the specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position (exclude the cosθ=0∘)Solution in Gujrati
The force acting on the plane are shown in the ure. The height of water level is l=0.5m. The length of the plank is 1.0=2l. The weight of the lane acts through the centre B of the plank. We have OB=l. The buoyant fore F acts through the point A which is the middle point of the dipped part OC of the plank.
We have OA=OC2=l2cosθ
Let the mass per unit length of the plane be rho.<br>itweightmg=2lrhog.<br>ThemassofthepartOCoftheplank=(l/(costheta))rho.<br>Themassofwaterdisplaced=1/0.5 l/(costheta)rho=(2/p)/(costheta)<br>ThebuoyantforceFis∴F=(2lrhog)/(costheta)<br>Nowforequilibriumthe→rqueofmgaboutOshod––balancethe→rqueofFaboutO.<br>So, mg(OB)sintheta=F(OA)sintheta<br>or , (2lrho)=((2lrho)/(costheta))(l/(2costheta))<br>or, cos^2theta= 1/2<br>or costheta=1/sqrt2, or theta=45^@
Similar Questions
A uniform plank of length 4m and weighing 50kg is supported at two knife edges each at 1m from the ends of the plank. How close to the end of the plank can a man weighing 70kg walk before it tips.
View SolutionA uniform wooden plank of mass 150 kg and length 8 m is floating on still water with a man of 50 kg at one end of it . The man walks to the other end of the plank and stops. Than the distance covered by the plank is
View SolutionThe wooden plank of length 1 m and uniform cross section is hinged at one end to the bottom of a tank as shown in figure. The tank is filled with water up to a height of 0.5 m. The specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position. (Exclude the case θ=0)
 ,
,
View SolutionA wooden rod of a uniform cross section and of length 120 cm in hinged at the bottom of the tank which is filled with water to a height of 40cm. In the equilibrium position, the rod makes an angle of 60∘ with the vertical. The centre of buoyancy is located on the rod at a distance (from the hinge) of
View SolutionA wooden plank of length 1m and uniform cross-section is hinged at one end to the bottom of a tank as shown in fig. The tank is filled with water upto a hight 0.5m. The specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position. (Exclude the case θ=θ∘)

View SolutionA uniform rod of length 2.0 m specific gravity 0.5 and mass 2 kg is hinged at one end to the bottom of a tank of water (specific gravity = 10) filled upto a height o f 1.0 m as shown in figure. Taking the case θ=−0∘ the force exerted by the hings on the rod is (g=10m/s2)
View SolutionA wooden rod of a uniform cross section and of length 120cm is hinged at the bottom of the tank which is filled with water to a height of 40cm. In the equilibrium position, the rod makes an angle of 60∘ with the vertical. The centre of buoyancy is located on the rod at a distance (from the hinge) of
View SolutionA uniform wooden plank of mass 150 kg and length 8 m is floating on still water with a man of 50 kg at one end of it . The man walks to the other end of the plank and stops. Than the distance covered by the plank is
View Solution
