A uniform disc of radius R is put over another unifrom disc of radius 2R of the same thickness and density. The peripheries of the two discs touch each other. Locate the centre of mass of the system.Solution in Gujrati
Let the centre of the bigge disc be the origin.
2R=Radiusofbig≥rdisc<br>R=Radiusofsmal≤rdisc
m1=μRxT×ρ
m2=μ(2R)2×T×ρ
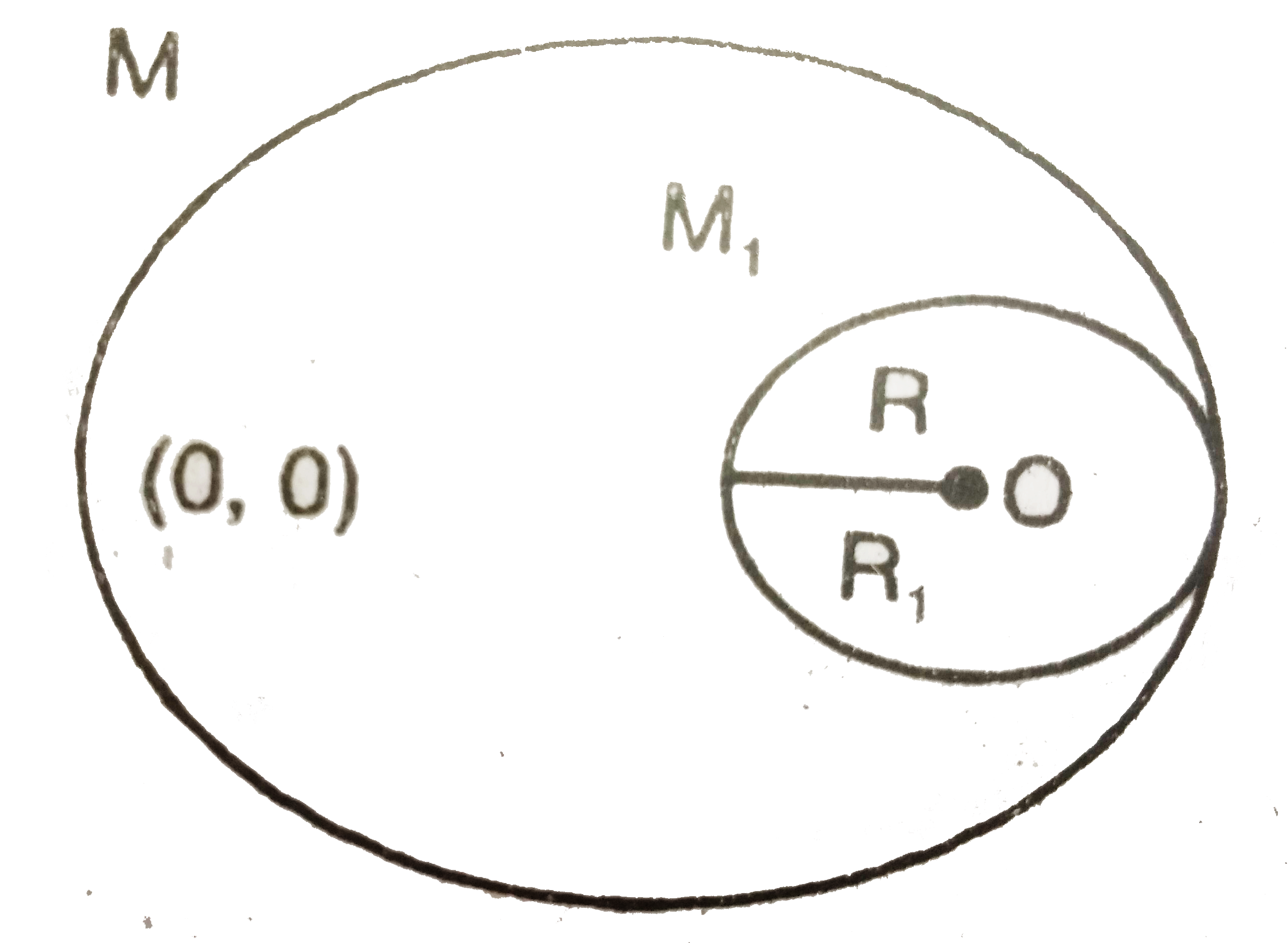
whereT=Thick≠ssofthetwodiscs<br>rho=Density of the two discs<br>:.Positionofthecentreofmass<br>((m_1x_1+m_2x_2)/(m_1+m_2),(m_1y_1+m_2y_2)/(m_1+m_2))<br>x_1=R,y_1=0<br>x_2=0, y_2=0<br>((piR^2TrhoR+0)/(muR^2TrhoR+mu(2R)^2Trho),0/(m_1+m_2))<br>((piR^2TrhoR)/(5muR^2Trho))=(R/4,0)<br>AtR/5 from the centre of bigger disc towards.
Similar Questions
A uniform disc of diameter R/2 is put over another uniform disc of radius R of same thickness and density. The peripheries of the two disc touch each other. The centre of mass of the system from centre of big disc is
View SolutionA uniform disc of diameter R/2 is put over another uniform disc of radius R of same thickness and density. The peripheries of the two discs touch each other. Locate the centre of mass of the system.
View SolutionA disc of radius R is cut out from a larger disc of radius 2R in such a way that the edge of the hole touches the edge of the disc. Locate the centre of mass of the remaing portion.
View SolutionA uniform disc of radius R is put over another uniform disc of radius 2R of same thickness and density. The peripheres of the two discs touch eachother. The position of their centre of mass is
View SolutionA uniform disc of diameter R/2 is put over another uniform disc of diameter R of same thickness and density. The peripheries of the two discs touch each other. The centre of mass of the system from centre of big disc is
View SolutionThree circular discs of same material and same thickness of radii r, 2r and 3r are placed on a horizontal plane such that their centres lie along a straight line. The radius of the middle disc is 2r and it touches the other two discs. The distance of the centre of mass of the system from the centre of the smaller disc is
View SolutionA disc of radius R is cut from a larger disc of radius 2R in such a way that the edge of the hole touches the edge of the disc. The centre of mass of the remaining portion is at
View SolutionA uniform disc of radius R is put over another uniform disc of radius 2R of same thickness and density. The peripheres of the two discs touch eachother. The position of their centre of mass is
View Solution
