A hemispherical bowl of radius R is set rotating about its axis of symmetry which is kept vertical. A small block kept in the bowl rotates with the bowl without slipping on its surface. If the surfaces of the bowl is smooth, and the angle made by the radius through the block with the vertical is $θ$ , find the angular speed at which the bowl is rotating.Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C

If et bowl rotates at maximum angular speed, the block tends to slip upwards.
So the frictioN/Al force acts downward.
Here, $r = R sin θ$
From the free body diagram 1
$R_{1} - m g cos θ - m ω^{2}_1 (R sin θ) sin θ$
$= 0 \dots \dots \dots . i$
[because $r = R sin θ]$ and
$μ R_{1} + m g sin θ - m ω^{2}_1 (R sin θ) cos θ$
=0 ii.

Substituting the value of $R_{1}$ from equation i. inequation ii it can be found out that
$ω_{1} = \frac{(g (sin θ) + μ cos θ)}{R sin θ (cos θ - μ sin θ)}]^{\frac{1}{2}}$
again, for minimum speed, the frictioN/Asl force $μ R_{2}$ acrts upwasrd,. From free body diagram -2, it can be prove that

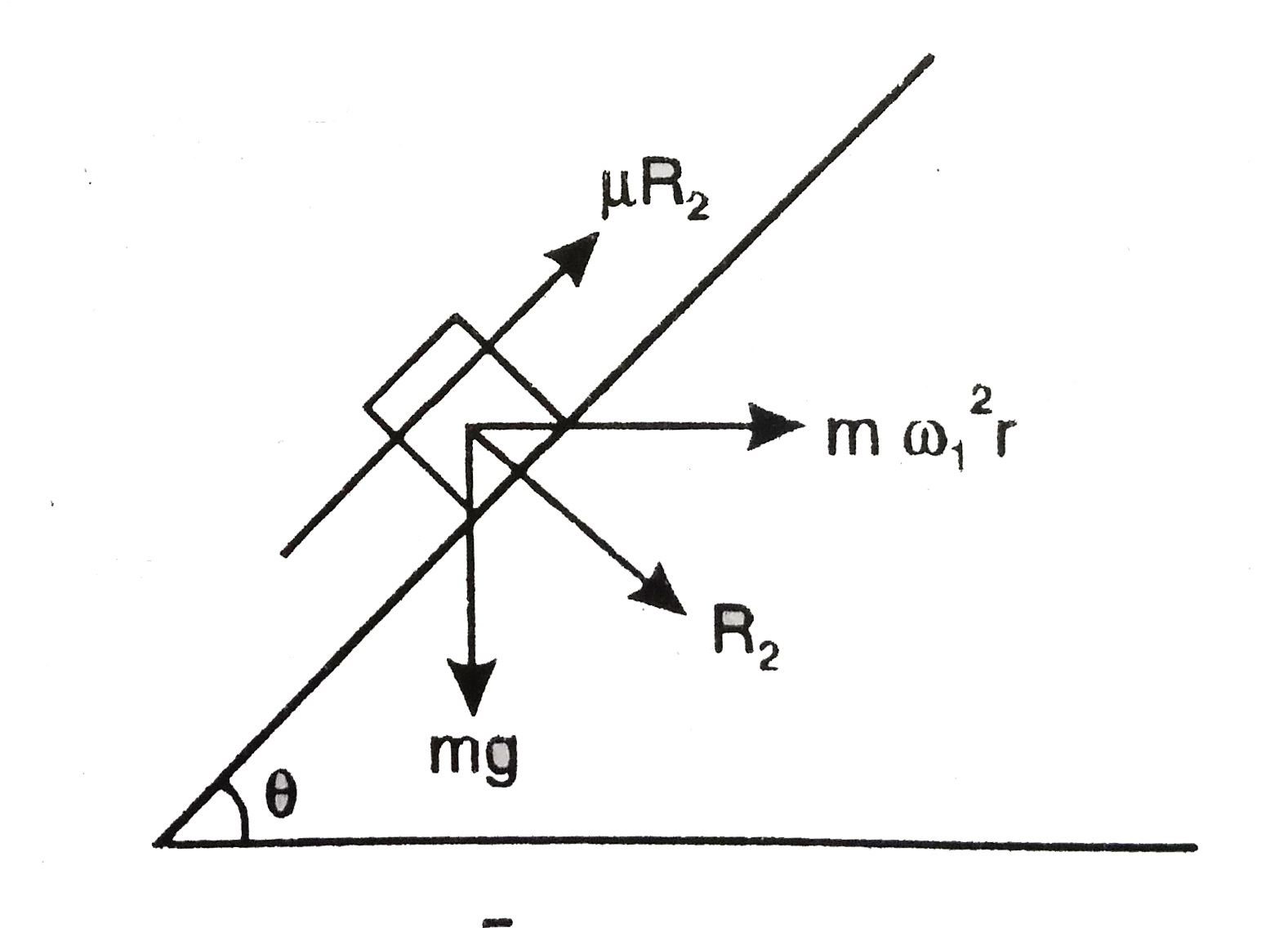
$ω_{2} = {[\frac{g (sin θ + μ cos θ)}{R sin θ (cos t h e t - μ sin θ)}]}^{\frac{1}{2}}$
$∴$ the range of speed is betwen $ω_{2} and ω_{1}$

Updated on:21/07/2023

|

Class 11 PHYSICS CIRCULAR MOTION

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile