A block is kept inside a hemispherical bowl rotating with angular velocity ω. Inner surface of bowl is rough, coefficient of friction is μ. The block is kept at a position where radius makes an angle θ with the vertical. What is the range of the angular speed for which the block will stay at the given position?
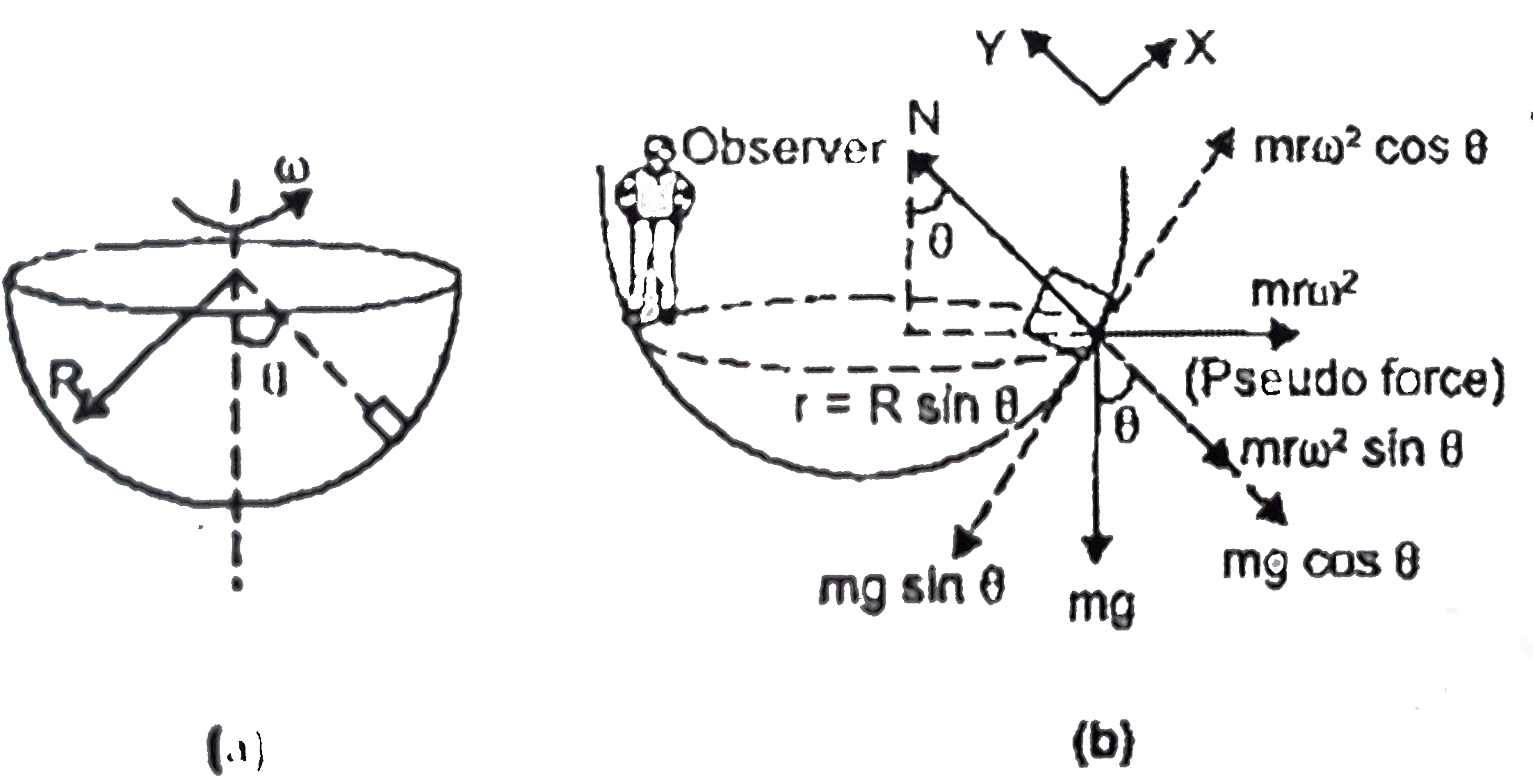
Step by step video & image solution for A block is kept inside a hemispherical bowl rotating with angular velocity omega. Inner surface of bowl is rough, coefficient of friction is mu. The block is kept at a position where radius makes an angle theta with the vertical. What is the range of the angular speed for which the block will stay at the given position? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FORCE ANALYSISBook:ANURAG MISHRAChapter:FORCE ANALYSISExercise:level 1
Explore 103 Videos
- FORCE ANALYSISBook:ANURAG MISHRAChapter:FORCE ANALYSISExercise:Level-2
Explore 73 Videos
- FORCE ANALYSISBook:ANURAG MISHRAChapter:FORCE ANALYSISExercise:Matching type
Explore 13 Videos
- DESCRIPTION OF MOTIONBook:ANURAG MISHRAChapter:DESCRIPTION OF MOTIONExercise:Level-3
Explore 34 Videos
- IMPULSE AND MOMENTUMBook:ANURAG MISHRAChapter:IMPULSE AND MOMENTUMExercise:matching
Explore 3 Videos
Similar Questions
A disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

View SolutionA hemisphericla bowl of rdius R is rotated about its axis of symetry which is kept vertical.A small block is kept in the bowl at a position where the radius makes an angle θ with the vertical. The block rottes with the bowl without any sliping. The friction coefficient between the block and teh bowl surface is μ. Find the range of the angular speed for which the block will not slip.
View Solution
Knowledge Check
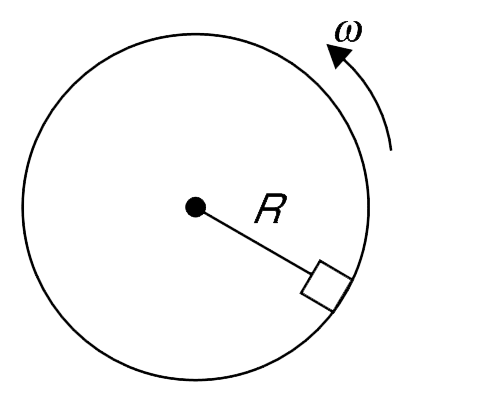
A body of mass m and radius r is rotated with angular velocity ω as shown in the figure & kept on a surface that has sufficient friction then the body will move
 Abackwards first and then move forwardBforward first and then move backwardCwill always move forwardDnone of these
Abackwards first and then move forwardBforward first and then move backwardCwill always move forwardDnone of theseA spherical bowl of radius R rotates about the verical diameter with angular velocity ω.The bowl contains a small object inside and in absence of friction, this object takes up a position inside the bowl such that its radius vector makes an angle θ with the vertical (see figure). Then
 Aω=√g/rcosθBω=2πg/rCω=√gcosθrDω=√rcosθ×g
Aω=√g/rcosθBω=2πg/rCω=√gcosθrDω=√rcosθ×gA ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
Aω0μR2gBω0g2μRC2ω0RμgDω0R2μg
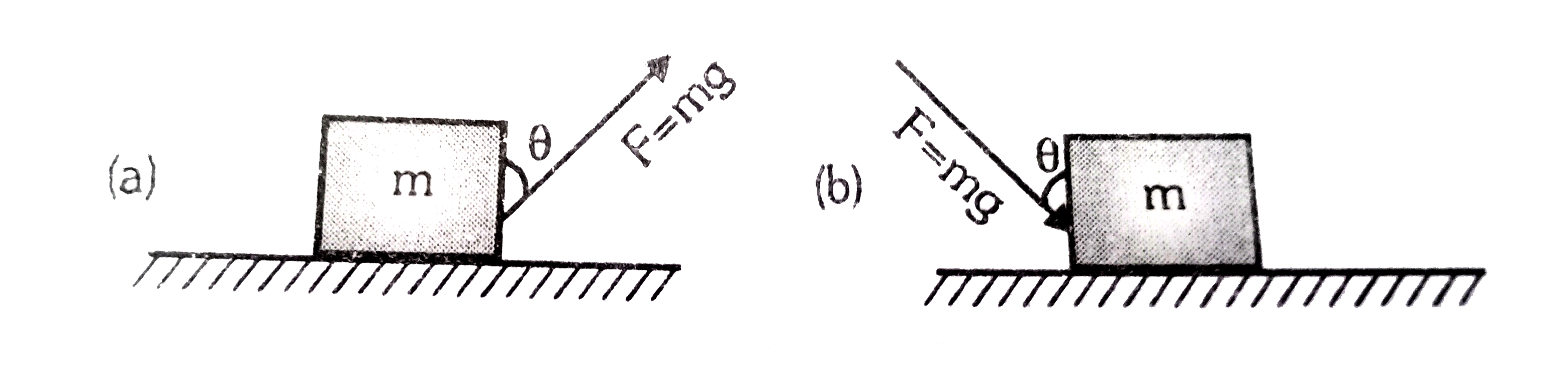
A block of mass m rests on a rough horizontl surface as shown in figure (a) and (b). Coefficient of friciton between block and surface is μ. A force F-mg acting at an angle θ with the vertical side of the block. Find the condition for which block will move along the surface.
View SolutionA hemispherical bowl of radius R is set rotating about its axis of symmetry which is kept vertical. A small block kept in the bowl rotates with the bowl without slipping on its surface. If the surfaces of the bowl is smooth, and the angle made by the radius through the block with the vertical is θ, find the angular speed at which the bowl is rotating.
View SolutionA cylinder with radius R spins about its horizontal axis with angular speed ω. There is a small block lying on the inner surface of the cylinder. The coefficient of friction between the block and the cylinder is μ. Find the value of ω for which the block does not slip, i.e., stays at rest with respect to the cylinder.
View SolutionA block of mass M is at rest on a rough horizontal surface. The coefficient of friction between the block and the surface is μ. A force F = Mg acting at an angle θ with the vertical side of the block pulls it. In which of the following cases, the block can be pulled along the surface?
View SolutionA block of mass M rests on a rough horizontal surface as shown. Coefficient of friction between the block and the surface is μ. A force F=mg acting at angle θ with the vertical side of the block pulls it. In which of the following cases the block can be pulled along the surface?

View Solution
