Let denote the angular displacement of a simple pendulum oscillating in a vertical plane. If the mass of the bob is m, the tension in the string is Solution in Gujrati
The correct Answer is:A, C
At the extreem position, velocity of the pendulum is zeor,
So there is no centrifungal force
:. T=mg cos theta
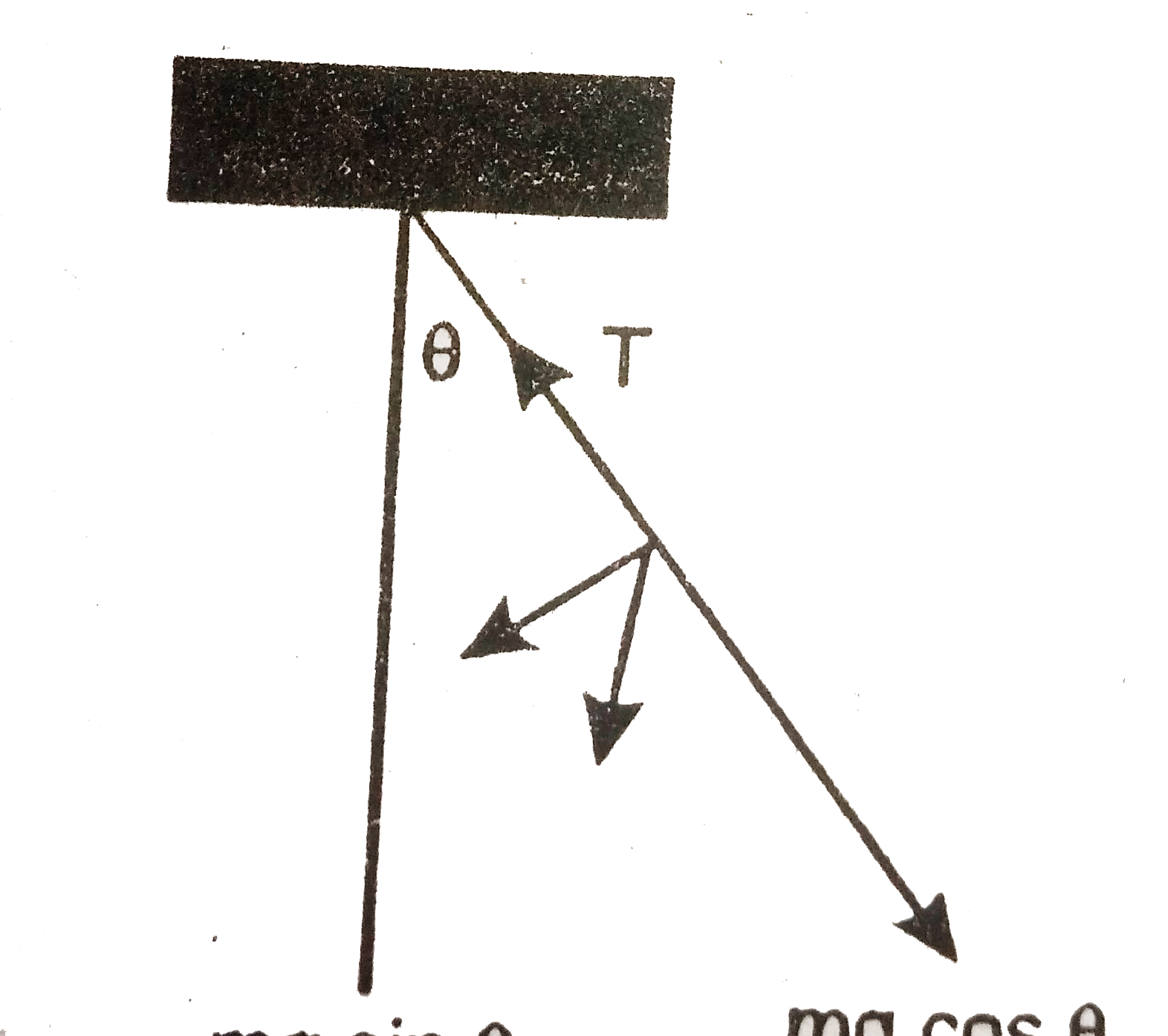
Similar Questions
the bob of simple pendulum is relasesd when string makes an angle theta with the vertical . If m be the mass of the bob then find the tension when the bob is at the bottiommost position .
View SolutionA simple pendulum with charged bob is oscillating with time period T and let θ be the angular displacement. If the uniform magnetic field is switched ON in a direction perpendicular to the plane of oscillation then
View SolutionA simple pendulum with charged bob is oscillating with time period T and let θ be the angular displacement. If the uniform magnetic field is switched ON in a direction perpendicular to the plane of oscillation then
View SolutionA simple pendulum of length L and bob of mas M is oscilating in a plane about a vertical line between angular limits - ϕ and ϕ. For an angular displacement θ. [|θ<ϕ|][|θ|<ϕ] the tension in the string and velocity of the bob are T And v respectively. The following relations hold good under the above conditions:
View SolutionLet be the angular displacement fixed by a simple solute when oscillating in the vertical plane. Tension in thread and thread mg cos theta If so:
View SolutionLet θ denote the angular displacement of a simple pendulum oscillating in a vertical plane. If the mass of the bob is m, the tension in the string is mgcosθ
View SolutionA simple pendulum of length L and mass (bob) M is oscillating in a plane about a vertical line between angular limit -phi and +phi . For an angular displacement theta(|theta|ltphi) , the tension in the string and the velocity of the bob are T and V respectively. The following relations hold good under the above conditions:
View SolutionA simple pendulum of length L and mass M is oscillating about a vertical line with angular amplitude θ. If for an angular displacement ϕ(ϕ>θ) the tension in the string is T1 and for angular amplitude θ the tension is T2, then
View Solution