The block shown in figure has a mass M and descends with an acceleration a. the mass of the string below the point A is m. Find the tension of the string at the point A and at the lower end.
 Solution in Gujrati
Solution in Gujrati
Consider the block +the part of the string below A'' as the system . Let the tension at A be T. The forces acting on this system are
a. (M+mg)g, downward, by the earth
T, upward, by the upper part of the string.
The first is gravitatioN/Al and the second is electromagnetic. We do not have to write the force by the string on the block. This electromagnetic force is by one part of the system on the other part. Only the forces acting on the system by the objects other than the system are to be included.
The system is descending with an acceleration a. Taking the downward direction as the X-axis, the total force along the X-axis is (M+m)g−T. Using Newton's law along the X-axis is (M+mg)g−T=(M+m)a.
or T=(M+m)(g−a)
we have omitted the free body diagram. This you can do if you can draw the free body diagram in your mind and write the equations correctly.
To get the tension T' at the lower end we can put m=0∈i.
Effectively we take the point A at the lower end. Thus, we get T'=M(g−a).
Similar Questions
The mass of the part of the string below A in figure is m. Find the tension of the string at the lower end and at A.
View SolutionThe block shown in figure has a mass M and descends with an acceleration a. The mass of the string below the point A is m. Find the tension of the string at the point A and at the lower end.

View Solutionfind the acceleration of the block of mass M in the situation shown in figure. All the surfaces are frictionless and the pulleys and the string are light.

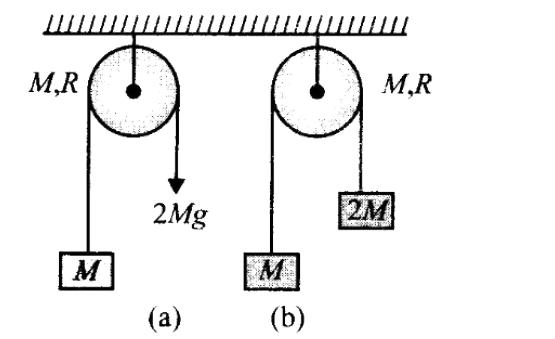
View Solutionजैसा कि आकृति में दिखाया गया है कि एक डोरी द्रव्यमान M और त्रिज्या R की घिरनी (चकती) पर लिपटी हुई है। डोरी के एक सिरे पर, द्रव्यमान M का एक गुटका जुड़ा है और दूसरे सिरे में (a) 2 Mg का बल और (b) द्रव्यमान 2 M का एक गुटका जुड़ा है। Aऔर B में क्रमश: αA और αB चकती के कोणीय त्वरण हैं, तब: (घिरनी पर डोरी फिसल नहीं रही है)
View SolutionA block of mass M is being pulled with the help of a string of mass m and length L. the horizontal force applied by the man on the string is F.

Determine
(a) Find the force exerted by the string on the block and acceleration of system.
(b) Find the tension at the mid point of the string.
(c ) Find the tension at a distance x from the end at which force is applied.
Assume that the block is kept on a frictionless horizontal surface and the mass is uniformly distributed in the string.
View SolutionA body of mass M is hanging by an inextensible string of mass m. If the free end of the string accelerates up with constant acceleration a. find the variation of tension in the string a function of the distance measured from the mass M (bottom of the string).

View SolutionFigure shown a block of mass m placed on a smooth wedge of mass M. Calculate the minimum value of M' and tension in the string, so that the block of mass m will move vertically downwards with acceleration 10ms^(-2)
View SolutionA block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R figure a. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
View Solution