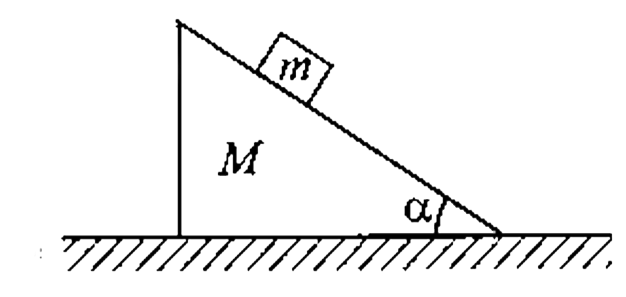
Figure shown a block of mass m placed on a smooth wedge of mass M. Calculate the minimum value of M' and tension in the string, so that the block of mass m will move vertically downwards with acceleration 10ms−2
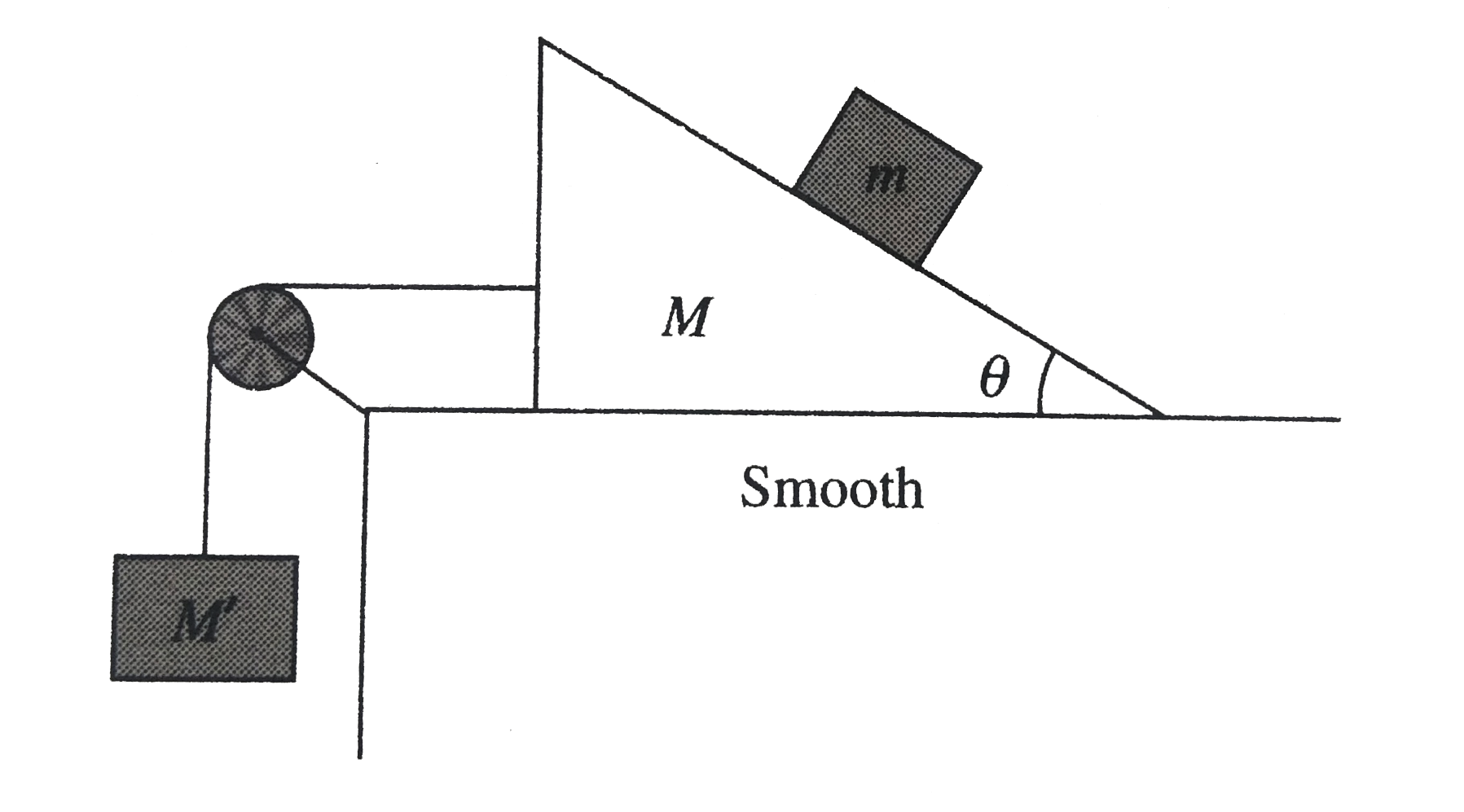
The value of M' is Mcotθ1−cotθ
The value of M' is Mtanθ1−tanθ
The value of tension in the string is Mgtanθ
The value of tension is Mgcotθ
The correct Answer is:A, C
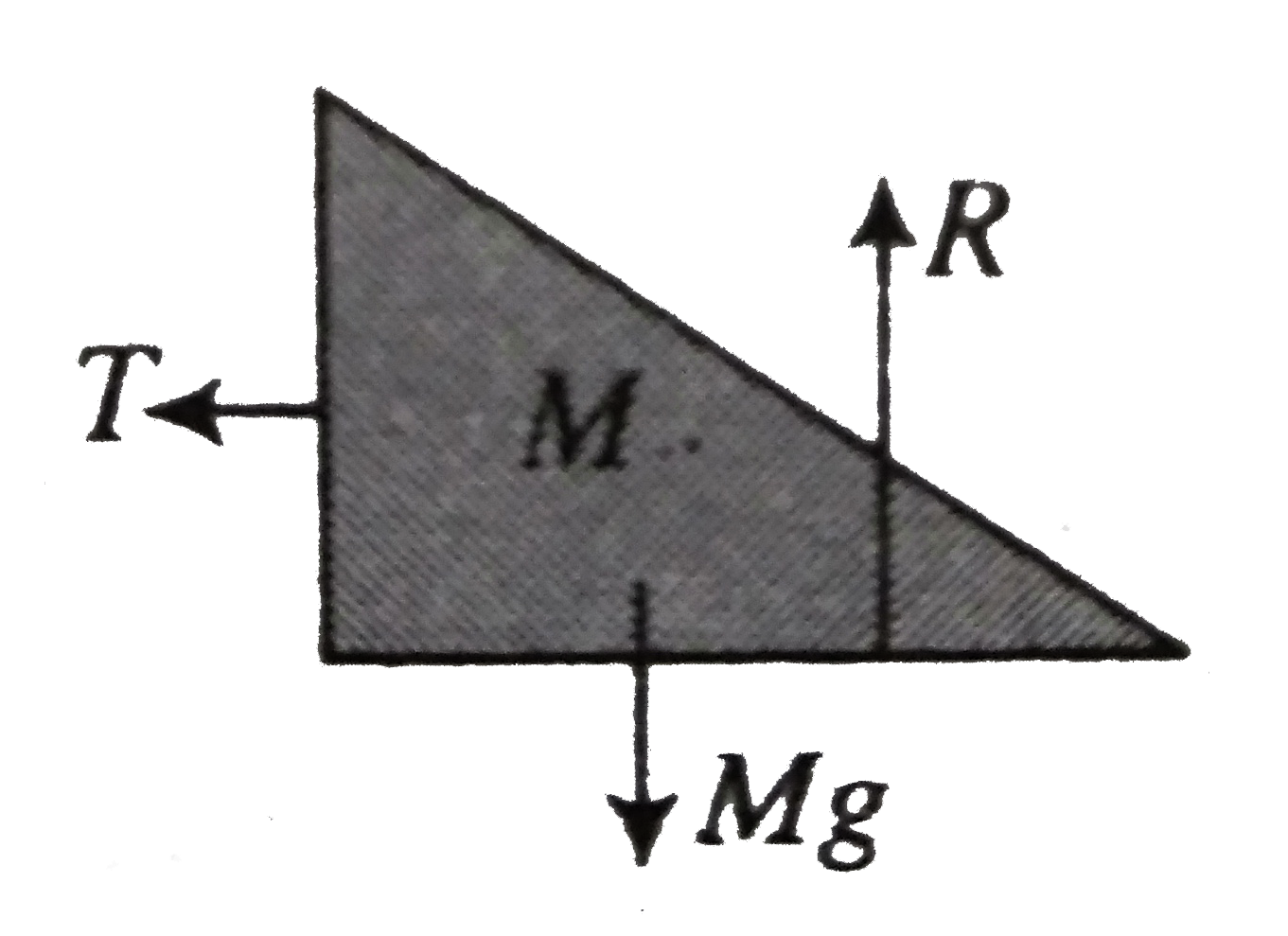
M'g−T=M'a ...(i)
T=Ma ...(ii)
M'g=a(M+M')
⇒a=M'g(M+M')
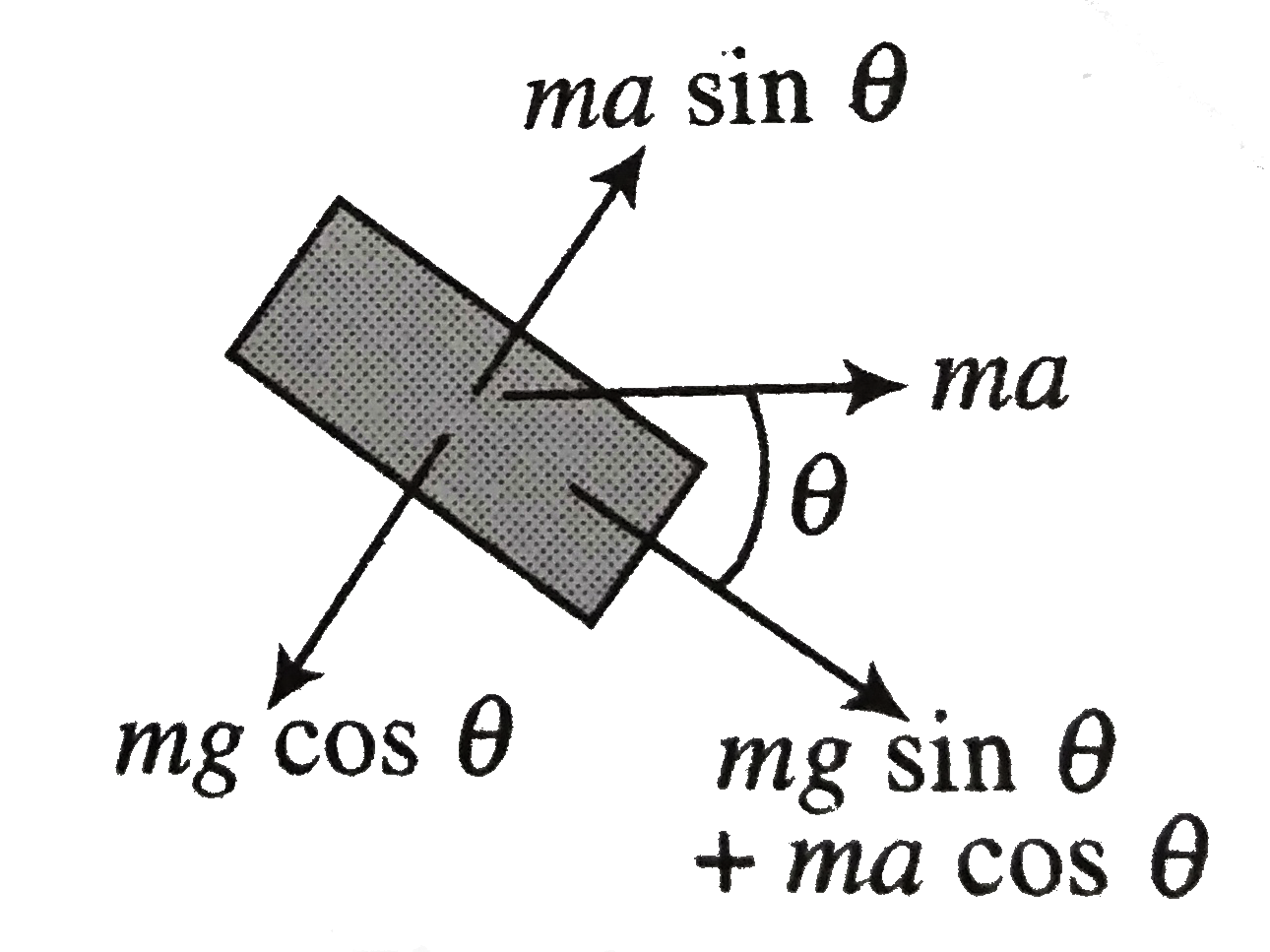
masinθ=mgcosθ→ so that normal force is zero.
a=gcotθ
gcotθ=M'g(M+M')⇒cotθM+cotθM'=M'
or M'=Mcotθ(1−cotθ), T=Ma=Mgcotθ=Mg/tanθ.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Assertion-reasoning
Explore 15 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Linked Comperhension
Explore 46 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Single Correct
Explore 76 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
Similar Questions
Fig shows a block of mass 0.1kg placed on a smooth wedge of mass 15√3 kg if the block of mass m will move vertically downward with acceleration 10m/s2 Then the value of tension (in newton) in the string is (θ=30∘) :
View SolutionFigure-2.54 shows a block of mass m is placed on an inclined wedge of mass M If the system is released from rest find the acceleration of m and M.
View Solution
Knowledge Check
A block of mass 3m is suspended by a meter scale rod of mass m as shown in figure. If the tension in the string A is equal to kmg in equilibrium, then value of k will be
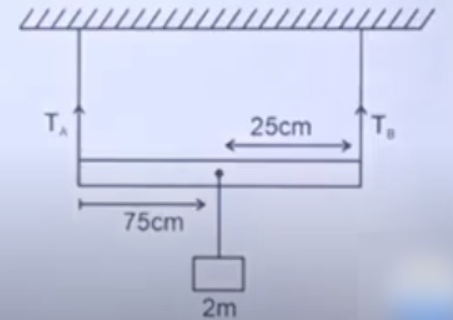 A43955B43926C43895D43835
A43955B43926C43895D43835The block of mass m is at rest. Find the tension in the string A .
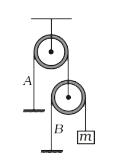 AmgB2 mgC3 mgD4 mg
AmgB2 mgC3 mgD4 mgThe figure shows a block of mass M=2m having a spherical smooth cavity of radius R placed on a smooth horizontal surface .There is a small ball of mass m moving at an instant vertically downward with a velocity v with respect to the block .At this instant :
 AThe normal reaction on the ball by the block is mv2RBThe normal reaction on the ball by the block is 23mv2RCThe acceleration of the block with respect to the ground is v23RDThe acceleration of the block with respect to the ground is v22R
AThe normal reaction on the ball by the block is mv2RBThe normal reaction on the ball by the block is 23mv2RCThe acceleration of the block with respect to the ground is v23RDThe acceleration of the block with respect to the ground is v22R
A block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

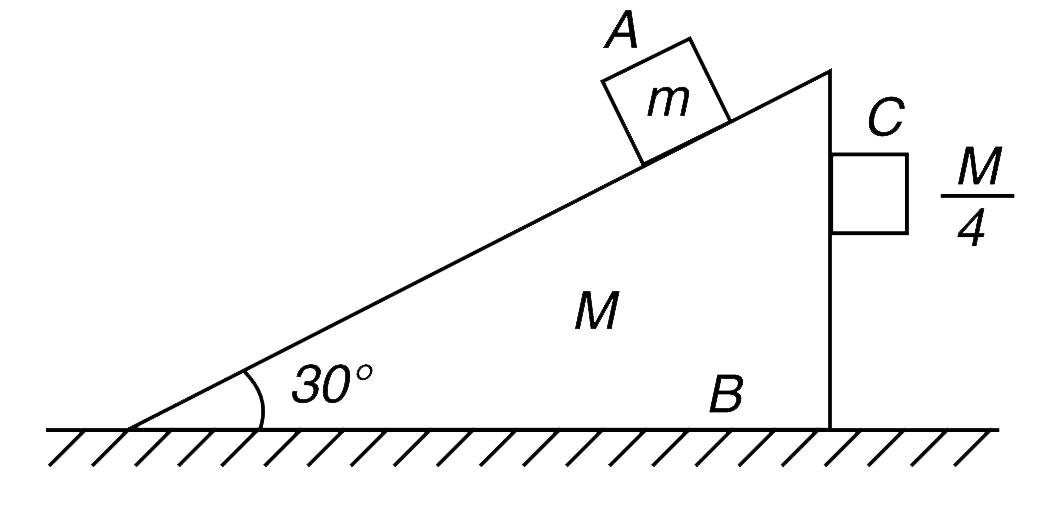
View SolutionIn the arrangement shown in figure, a block A of mass m has been placed on a smooth wedge B of mass M. The wedge lies on a horizontal smooth surface. Another block C of mass M4 has been placed in contact with the wedge B as shown. The coefficient of friction between the block C and the vertical wedge wall is μ=34. Find the ratio mM for which the block C will not slide with respect to the wedge after the system is released?
View SolutionA block of mass m is released from a wedge of mass m as shown in figure . Find the time taken by the block to reach the end of the wedge.
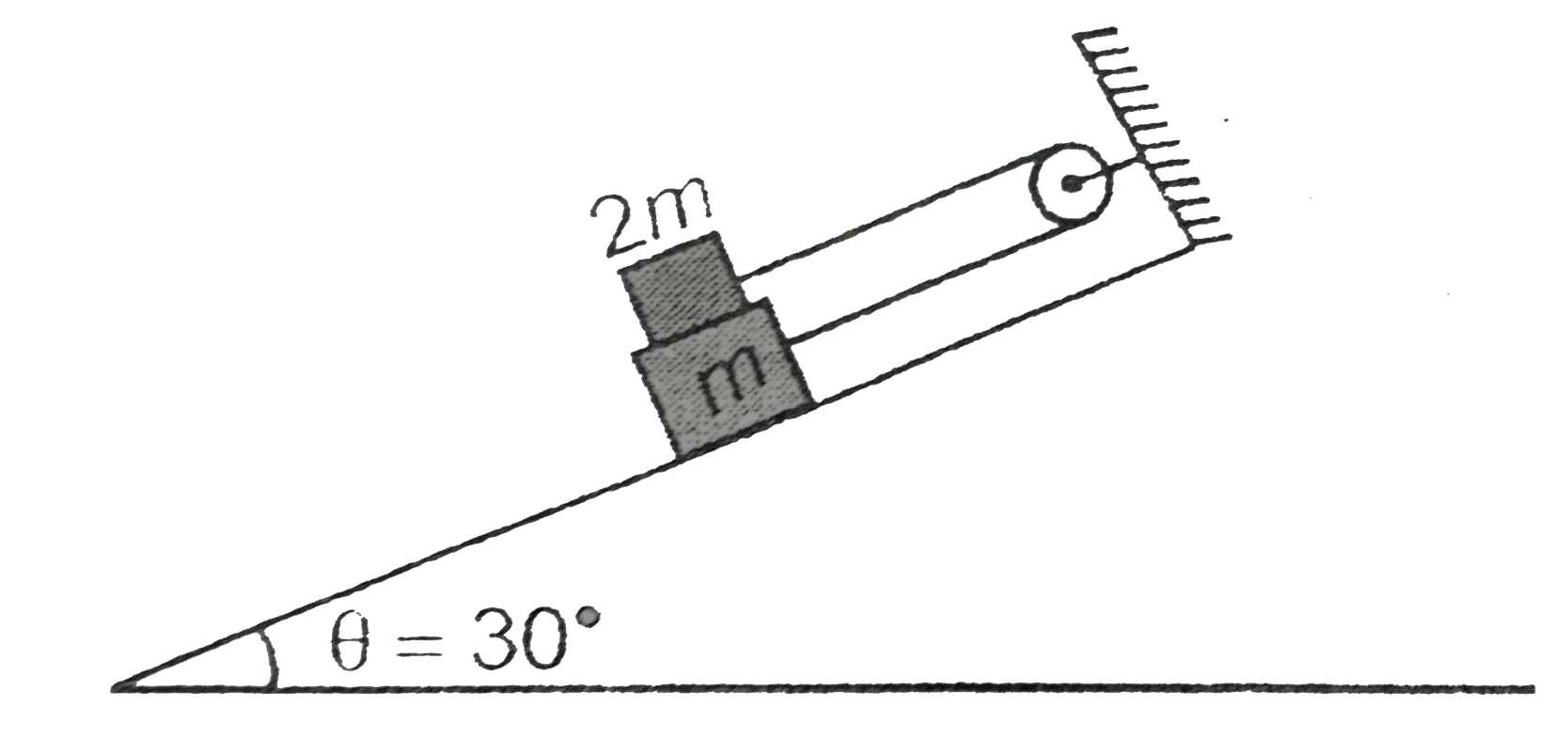
View SolutionFigure shows a block of mass 2m sliding on a block of mass m. Find the acceleration of each block . ( All surface are smooth )
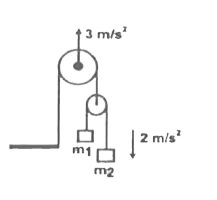
View SolutionIn the figure shown, the acceleration of block of mass m2 is 2m/s2. The acceleration of m1 :
View Solution

