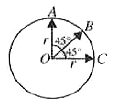
Find the resultant of the three vectors $- - \to O A, - - \to O B$ and $- - \to O C$ shown in figure. Radius of the circle is R.
Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

OA=OC
$- - \to O A + (O C)$ is along $- - \to O B$ (bisector ) and its magnitude is
$2 R {cos 45}^{0} = R \sqrt{2}$
$- ---------- \to (O A) + (\to O C) + - - \to O B$ and its magnitude is
$R \sqrt{2} + R = R (1 + \sqrt{2})$

Updated on:21/07/2023

|

Class 11 PHYSICS BASIC MATHEMATICS

Similar Questions

Find the resultant of the vectors vec(OA), vec(OB), vec(OC) as shown in figure. The radius of the circle is r.
View Solution
Find the resultant of the vectors $- - \to O A, - - \to O B, - - \to O C$ as shown in figure. The radius of the circle is r.
View Solution
The magnitude of vectors $- - \to O A, - - \to O B and - - \to O C$ in figure are equal. Find the direction of $- - \to O A + - - \to O B - - - \to O C$ .
.
View Solution
Find the resultant of the three vectors $- - \to O A, - - \to O B$ and $- - \to O C$ shown in figure. Radius of the circle is R.

View Solution
Find the resultant of the vectors $- - \to O A, - - \to O B, - - \to O C$ as shown in figure. The radius of the circle is r.
View Solution
The resultant of the three vectors $- - \to O A, - - \to O B$ and $- - \to O C$ shown in figure is

View Solution
Find the resultant of the three vectors $- - \to O A, - - \to O B$ and $- - \to O C$ shown in figure. Radius of the circle is R.

View Solution
Find the resultant of the three vectors $- - \to O A, - - \to O B$ and $- - \to O C$ shown in figure. Radius of the circle is R.

View Solution

Recommended Questions

Home
Ask Doubt
Profile