The resultant of the three vectors −−→OA,−−→OB and −−→OC shown in figure is
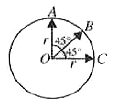
r
2r
r(1+√s)
r(√2−1)
The correct Answer is:C
−−→OC and −−→OA are cqual in magnitude and inclined to each other at an angle of 90∘. So their resultant is √2r. It acts mid-way between −−→OC and −−→OA, ie., along OB. Now, both r and √2r are along the same line and in the same direction .
Resultant = r+√2r=r(1+√2)
Topper's Solved these Questions
- KINEMATICS Book:MTG-WBJEEChapter:KINEMATICS Exercise:WB JEE WORKOUT ( CATEGORY 2 : Single Option Correct Type (2 Marks))
Explore 15 Videos
- KINEMATICS Book:MTG-WBJEEChapter:KINEMATICS Exercise:WB JEE WORKOUT ( CATEGORY 3 : One or More than One Option Correct Type (2 Marks))
Explore 10 Videos
- HEAT AND THERMAL PHYSICSBook:MTG-WBJEEChapter:HEAT AND THERMAL PHYSICSExercise:WB JEE PREVIOUS YEARS QUESTIONS
Explore 15 Videos
- KINETIC THEORY OF GASES Book:MTG-WBJEEChapter:KINETIC THEORY OF GASES Exercise:WB JEE PREVIOUS YEARS QUESTIONS (MCQ)
Explore 7 Videos
Similar Questions
Knowledge Check
What is the angle between the vector →A and →B as shown in figure ?
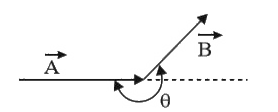 AθBπ−θCθ−πD2π−θ
AθBπ−θCθ−πD2π−θThe resultant of two vectors →P and →Q is →R. If the magnitude of →Q is doubled, the new resultant vector becomes perpendicular to →P. Then, the magnitude of →R is equal to
AP+QBPCP−QDQThe resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitudes is equal to half of the magnitudes of vector →B (figure). The angle between →A and →B is
 A120∘B150∘C135∘DNone of these
A120∘B150∘C135∘DNone of these
The magnitude of vectors −−→OA,−−→OBand−−→OC in figure are equal. Find the direction of −−→OA+−−→OB−−−→OC.
 .
.
View SolutionThe resultant of vectors −−→OAand−−→OB is peerpendicular to vec(OA). Find the angle AOB.
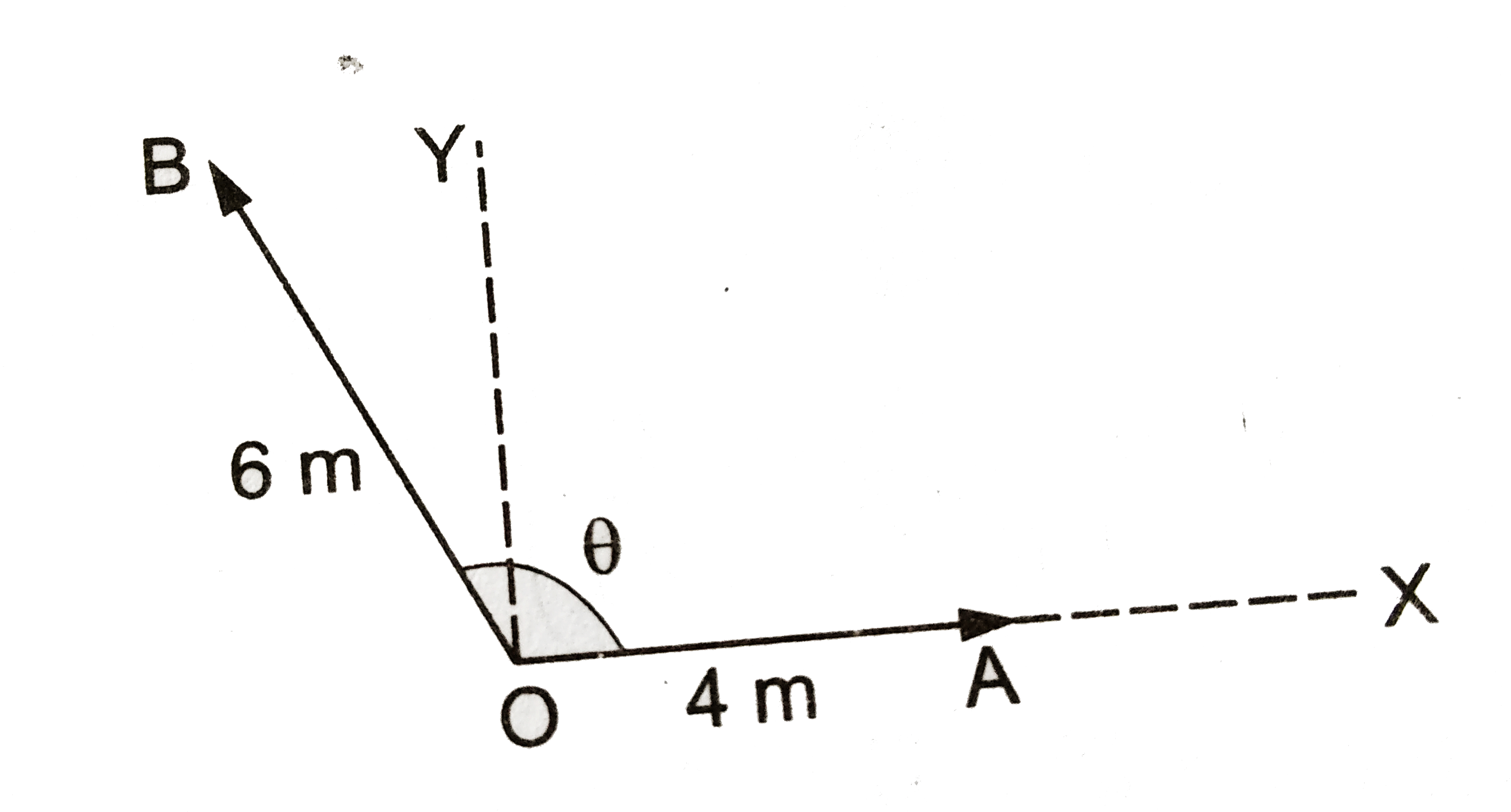
View SolutionABCD is a quadrilateral and E is the point of intersection of the lines joining the middle points of opposite side. Show that the resultant of −−→OA , −−→OB , −−→OC and −−→OD = 4 −−→OE , where O is any point.
View SolutionThe magnitudes of vectors −−→OA,−−→OB and −−→OC in figure(2-W3) are equal. Find the direction of −−→OA+−−→OB−−−→OC.
View SolutionThe resultant of two vectors →P and →Q is →R. If →Q is doubled then the new resultant vector is perpendicular to →P. Then magnitude of →R is :-
View Solution


