Marks scored by Sumit is 12.5% more than Sahil's marks. Ajay got 623% more marks then Sumit's. If difference between marks scored by Ajay and Sahil is 40, then find the total marks scored by all three.
A)665
B)450
C)555
D)745
The correct Answer is:A
To solve the problem step by step, we will define the marks scored by each student in terms of Sahil's marks and then find the total marks scored by all three students.
Step 1: Define Sahil's Marks
Let Sahil's marks be denoted as S.
Step 2: Calculate Sumit's Marks
According to the problem, Sumit scored 12.5% more than Sahil. We can express this mathematically:
Sumit's Marks=S+0.125S=1.125S
Thus, Sumit's marks can be written as:
Sumit's Marks=98S
Step 3: Calculate Ajay's Marks
Ajay scored 623% more than Sumit. First, we convert 623% into a fraction:
623%=203%
This can be expressed as:
Ajay's Marks=Sumit's Marks+20300×Sumit's Marks = 20300×98S
Calculating this gives:
Ajay's Marks=98S+215×98S=98S(1+215)
Finding a common denominator:
1+215=1515+215=1715
Thus, Ajay's marks can be written as:
Ajay's Marks=98S×1715=153120S
Step 4: Set Up the Equation for the Difference
According to the problem, the difference between Ajay's and Sahil's marks is 40:
Ajay's Marks−Sahil's Marks=40
Substituting the expressions we derived:
153120S−S=40
This simplifies to:
(153120−120120)S=40
33120S=40
Step 5: Solve for Sahil's Marks
Now, we can solve for S:
S=40×12033=480033≈145.45
Step 6: Calculate Sumit's and Ajay's Marks
Now we can calculate Sumit's and Ajay's marks:
Sumit's Marks=98S=98×480033=540033≈163.64
Ajay's Marks=153120S=153120×480033=18480396≈185.45
Step 7: Calculate the Total Marks
Finally, we add all the marks together:
Total Marks=S+Sumit's Marks+Ajay's Marks=480033+540033+18480396
Finding a common denominator and calculating gives:
Total Marks≈665
Final Answer
The total marks scored by all three is 665.
---
Let Sahil's marks be denoted as S.
According to the problem, Sumit scored 12.5% more than Sahil. We can express this mathematically:
Sumit's Marks=S+0.125S=1.125S
Thus, Sumit's marks can be written as:
Sumit's Marks=98S
Ajay scored 623% more than Sumit. First, we convert 623% into a fraction:
623%=203%
This can be expressed as:
Ajay's Marks=Sumit's Marks+20300×Sumit's Marks = 20300×98S
Calculating this gives:
Ajay's Marks=98S+215×98S=98S(1+215)
Finding a common denominator:
1+215=1515+215=1715
Thus, Ajay's marks can be written as:
Ajay's Marks=98S×1715=153120S
According to the problem, the difference between Ajay's and Sahil's marks is 40:
Ajay's Marks−Sahil's Marks=40
Substituting the expressions we derived:
153120S−S=40
This simplifies to:
(153120−120120)S=40
33120S=40
Now, we can solve for S:
S=40×12033=480033≈145.45
Now we can calculate Sumit's and Ajay's marks:
Sumit's Marks=98S=98×480033=540033≈163.64
Ajay's Marks=153120S=153120×480033=18480396≈185.45
Finally, we add all the marks together:
Total Marks=S+Sumit's Marks+Ajay's Marks=480033+540033+18480396
Finding a common denominator and calculating gives:
Total Marks≈665
The total marks scored by all three is 665.
Topper's Solved these Questions
- PERCENTAGEBook:ADDA247Chapter:PERCENTAGEExercise:PRELIMS QUESTIONS (LEVEL-2)
Explore 24 Videos
- PERCENTAGEBook:ADDA247Chapter:PERCENTAGEExercise:MAINS QUESTIONS
Explore 15 Videos
- PERCENTAGEBook:ADDA247Chapter:PERCENTAGEExercise:BASIC QUESTIONS
Explore 15 Videos
- NUMBER SYSTEM, SIMPLIFICATION AND APPROXIMATION Book:ADDA247Chapter:NUMBER SYSTEM, SIMPLIFICATION AND APPROXIMATION Exercise:PREVIOUS YEAR QUESTION
Explore 60 Videos
- PERMUTATION ,COMBINATION AND PROBABILITY Book:ADDA247Chapter:PERMUTATION ,COMBINATION AND PROBABILITY Exercise:Previous Year Question
Explore 25 Videos
Similar Questions
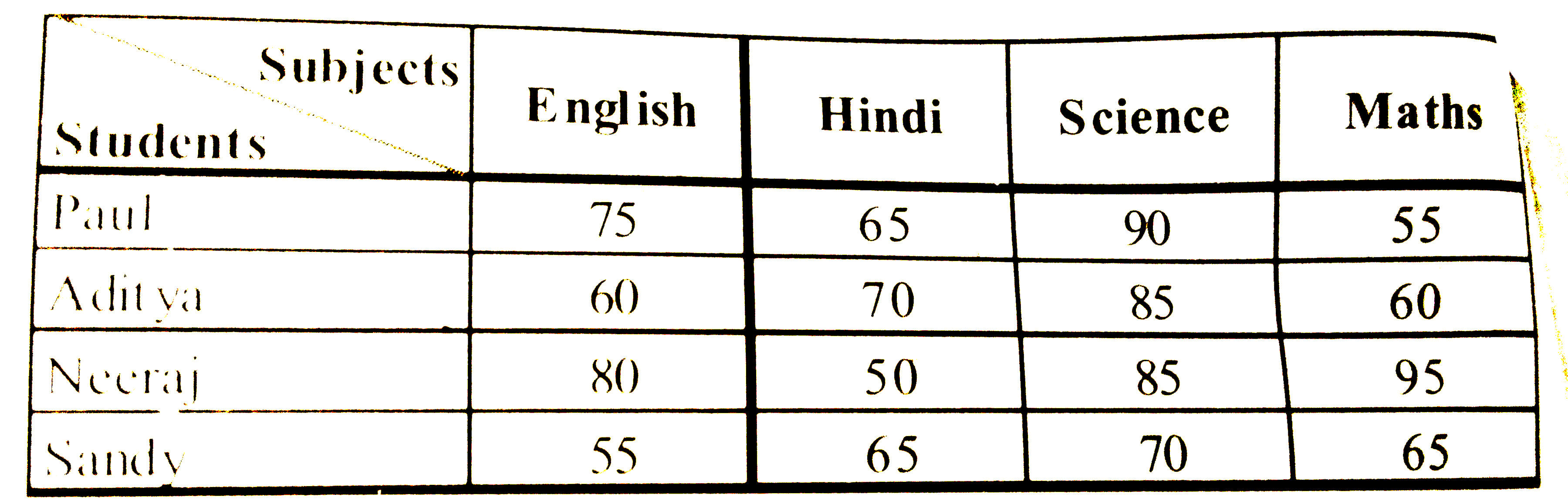
Total marks scored by Paoul are how much mreo/less than total marks scored by Neerja ?
View SolutionThe pie chart given shows the number of marks scored by a student in the given 5 subjects. The total marks scored by the student is 480.
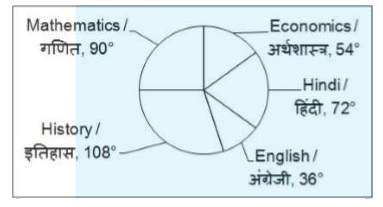
What is the difference between the marks scored by the student in Mathematics and the marks scored in Hindi?
View Solution
Knowledge Check
Ram aims to score an average of 80 marks in quarterly and half yearly exams. But his average in quarterly is 3 marks less than his target and that in half yearly is 2 marks more than his aim. The difference between the total marks scored in both the exams is 25. Total marks aimed by Ram is :
A400B410C420D380A student has to score 40% marks to get through. If he gets 40 marks and fails by 40 marks, then find the maximum marks set for the examination.
A200B250C300D150What are the marks scored by Abhijit in English?
I. Marks scored by Abhijit in Mathematics are more than his marks in Science by 20
II. Total marks scored by Abhijit in Mathematics, Science and English are 197.
III. Marks scored by Abhijit in Science are more than his marks in English by 12AAny two of the threeBII and IIICI, II and IIIDData is insufficient
In an examination, six subjects - S1, S2, S3, S4, S5, and S6 have equal maximum marks. The number of marks scored by one particular candidate in subject S1 is 20% less than his marks in subject S6. The ratio of marks scored by the same candidate in subject S2 to that in S3 is 4: 5 and that in S4 to S5 is 3: 4. The number of marks scored by this candidate in subject S5 is 25% more than that of S6. He scored 65 marks in the subject S3. He scored 436/9 % in the examination and the average of marks scored by him in all the subjects is 218/3
What percentage of marks the candidate had scored in the subject S5 over the maximum marks of that subject?
View SolutionIn an examination, six subjects - S1, S2, S3, S4, S5, and S6 have equal maximum marks. The number of marks scored by one particular candidate in subject S1 is 20% less than his marks in subject S6. The ratio of marks scored by the same candidate in subject S2 to that in S3 is 4: 5 and that in S4 to S5 is 3: 4. The number of marks scored by this candidate in subject S5 is 25% more than that of S6. He scored 65 marks in the subject S3. He scored 436/9 % in the examination and the average of marks scored by him in all the subjects is 218/3
Total marks scored by S2 and S3 is multiple of which of the following pairs.
View SolutionIn an examination, six subjects - S1, S2, S3, S4, S5, and S6 have equal maximum marks. The number of marks scored by one particular candidate in subject S1 is 20% less than his marks in subject S6. The ratio of marks scored by the same candidate in subject S2 to that in S3 is 4: 5 and that in S4 to S5 is 3: 4. The number of marks scored by this candidate in subject S5 is 25% more than that of S6. He scored 65 marks in the subject S3. He scored 436/9 % in the examination and the average of marks scored by him in all the subjects is 218/3
The number of marks obtained by the candidate in the subject S3 was how much percentage less than that of subject S5?
View SolutionIn an examination, six subjects - S1, S2, S3, S4, S5, and S6 have equal maximum marks. The number of marks scored by one particular candidate in subject S1 is 20% less than his marks in subject S6. The ratio of marks scored by the same candidate in subject S2 to that in S3 is 4: 5 and that in S4 to S5 is 3: 4. The number of marks scored by this candidate in subject S5 is 25% more than that of S6. He scored 65 marks in the subject S3. He scored 436/9 % in the examination and the average of marks scored by him in all the subjects is 218/3
The number of marks obtained by the candidate in the subject S2 was how much less than in the subject S4?
View SolutionIn an examination, six subjects - S1, S2, S3, S4, S5, and S6 have equal maximum marks. The number of marks scored by one particular candidate in subject S1 is 20% less than his marks in subject S6. The ratio of marks scored by the same candidate in subject S2 to that in S3 is 4: 5 and that in S4 to S5 is 3: 4. The number of marks scored by this candidate in subject S5 is 25% more than that of S6. He scored 65 marks in the subject S3. He scored 436/9 % in the examination and the average of marks scored by him in all the subjects is 218/3
What was the average of marks obtained by the candidate in the subject S5 and S6 together?
View Solution